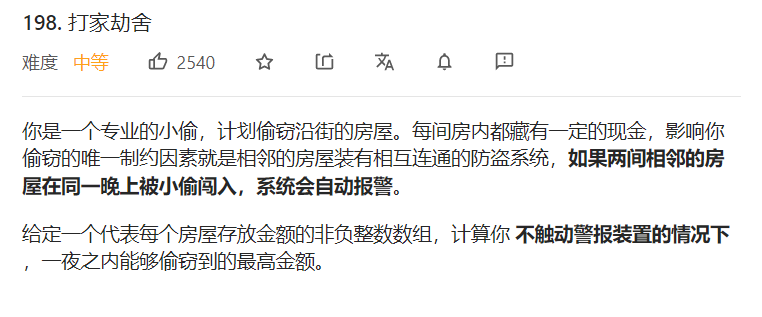
打家劫舍
示例 1:
1
2
3
4
| 输入:[1,2,3,1]
输出:4
解释:偷窃 1 号房屋 (金额 = 1) ,然后偷窃 3 号房屋 (金额 = 3)。
偷窃到的最高金额 = 1 + 3 = 4 。
|
示例 2:
1
2
3
4
| 输入:[2,7,9,3,1]
输出:12
解释:偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9),接着偷窃 5 号房屋 (金额 = 1)。
偷窃到的最高金额 = 2 + 9 + 1 = 12 。
|
代码为:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| class Solution {
public int rob(int[] nums) {
int n = nums.length;
if (n==0) return 0;
if (n==1) return nums[0];
int max =nums[0];
int dp[] = new int[n+1];
dp[1] = nums[0];
for (int i = 2;i<=n;i++){
dp[i] = Math.max(dp[i-1],dp[i-2]+nums[i-1]);
max = Math.max(dp[i],max);
}
return max;
}
}
|
上述方法使用了数组存储结果。考虑到每间房屋的最高总金额只和该房屋的前两间房屋的最高总金额相关,因此可以使用滚动数组,在每个时刻只需要存储前两间房屋的最高总金额。
代码为:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| class Solution {
public int rob(int[] nums) {
int n = nums.length;
if (n==0) return 0;
if (n==1) return nums[0];
if (n==2) return Math.max(nums[0],nums[1]);
int a = nums[0];
int b = Math.max(nums[0],nums[1]);
int c = 0;
for (int i = 2;i<n;i++){
c = b;
b = Math.max(b,a+nums[i]);
a = c;
}
return b;
}
}
|
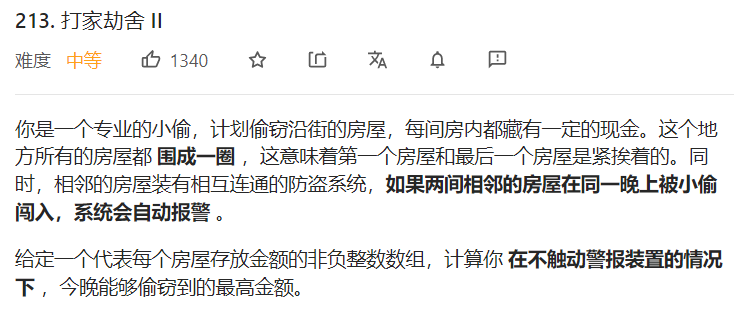
打家劫舍2
示例 1:
1
2
3
| 输入:nums = [2,3,2]
输出:3
解释:你不能先偷窃 1 号房屋(金额 = 2),然后偷窃 3 号房屋(金额 = 2), 因为他们是相邻的。
|
示例 2:
1
2
3
4
| 输入:nums = [1,2,3,1]
输出:4
解释:你可以先偷窃 1 号房屋(金额 = 1),然后偷窃 3 号房屋(金额 = 3)。
偷窃到的最高金额 = 1 + 3 = 4 。
|
示例 3:
+++++++++++++
此题与打家劫舍不同的是:唯一的区别是此题中的房间是 环状排列 的(即首尾相接),而 198.198. 题中的房间是 单排排列 的;而这也是此题的难点。

代码为:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| class Solution {
public int rob(int[] nums) {
int n = nums.length;
if (n==0) return 0;
if (n==1) return nums[0];
return Math.max(select(Arrays.copyOfRange(nums,0,n-1)),select(Arrays.copyOfRange(nums,1,n)));
}
public int select(int nums[]){
if (nums.length==0) return 0;
if (nums.length==1) return nums[0];
int dp[] = new int[nums.length+1];
int max = nums[1];
dp[1] = nums[0];
for (int i =2 ;i<=nums.length;i++){
dp[i] = Math.max(dp[i-1],dp[i-2]+nums[i-1]);
max = Math.max(max,dp[i]);
}
return max;
}
}
|
改进版:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| class Solution {
public int rob(int[] nums) {
int n = nums.length;
if (n==0) return 0;
if (n==1) return nums[0];
return Math.max(select(Arrays.copyOfRange(nums,0,n-1)),select(Arrays.copyOfRange(nums,1,n)));
}
public int select(int nums[]){
int a = 0;
int b = 0;
for (int num:nums){
int c = b;
b = Math.max(a+num,b);
a = c;
}
return b;
}
}
|
打家劫舍3
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| public int rob(TreeNode root) {
HashMap<TreeNode, Integer> memo = new HashMap<>();
return robInternal(root, memo);
}
public int robInternal(TreeNode root, HashMap<TreeNode, Integer> memo) {
if (root == null) return 0;
if (memo.containsKey(root)) return memo.get(root);
int money = root.val;
if (root.left != null) {
money += (robInternal(root.left.left, memo) + robInternal(root.left.right, memo));
}
if (root.right != null) {
money += (robInternal(root.right.left, memo) + robInternal(root.right.right, memo));
}
int result = Math.max(money, robInternal(root.left, memo) + robInternal(root.right, memo));
memo.put(root, result);
return result;
}
|
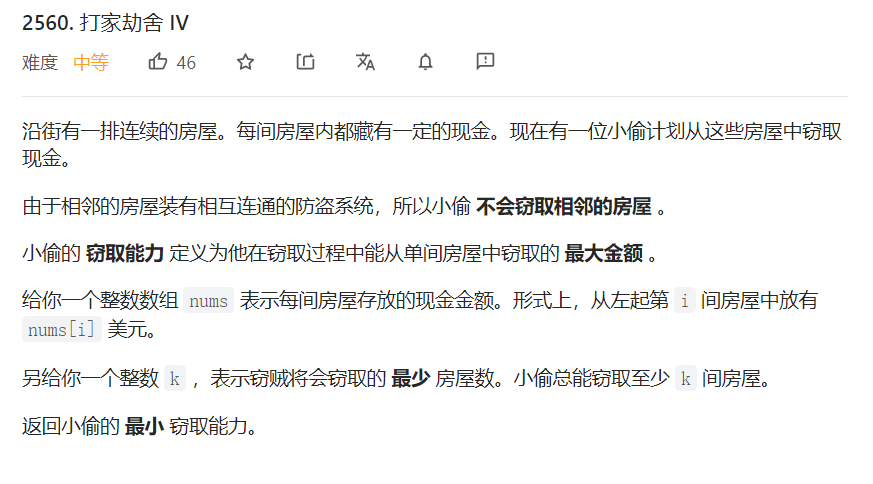
打家劫舍4
示例 1:
1
2
3
4
5
6
7
8
9
| 输入:nums = [2,3,5,9], k = 2
输出:5
解释:
小偷窃取至少 2 间房屋,共有 3 种方式:
- 窃取下标 0 和 2 处的房屋,窃取能力为 max(nums[0], nums[2]) = 5 。
- 窃取下标 0 和 3 处的房屋,窃取能力为 max(nums[0], nums[3]) = 9 。
- 窃取下标 1 和 3 处的房屋,窃取能力为 max(nums[1], nums[3]) = 9 。
因此,返回 min(5, 9, 9) = 5 。
|
示例 2:
1
2
3
| 输入:nums = [2,7,9,3,1], k = 2
输出:2
解释:共有 7 种窃取方式。窃取能力最小的情况所对应的方式是窃取下标 0 和 4 处的房屋。返回 max(nums[0], nums[4]) = 2 。
|
思路:最大化最小值 和 最小化最大值,就使用二分法
这题使用二分法+dp
(1)二分法:猜测可能的结果‘
(2)通过二分法猜测的结果,有多少个满足,是否大于k,如果大于则将在mid的左边继续,否则在mid的右边进行,。
代码为:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| class Solution {
public int minCapability(int[] nums, int k) {
int n = nums.length;
int l = 1;
int r = Arrays.stream(nums).max().getAsInt();
int dp[] = new int[n+1];
while (l<r){
int mid = (l+r)>>1;
if (nums[0]<=mid) {
dp[1] = 1;
}else dp[1] = 0;
for (int i = 2;i<=nums.length;i++){
if (nums[i-1]>mid){
dp[i] = dp[i-1];
}else {
dp[i] = Math.max(dp[i-2]+1,dp[i-1]);
}
}
if (dp[n]>=k){
r = mid;
}else {
l = mid+1;
}
}
return r;
}
}
|
优化:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| class Solution {
public static int minCapability(int[] nums, int k) {
int n = nums.length;
int l = 1;
int r = Arrays.stream(nums).max().getAsInt();
while (l<r){
int mid = (l+r)>>1;
int a = 0;
int b = nums[0]<=mid?1:0;
int c = 0;
for (int i = 2;i<=nums.length;i++){
if (nums[i-1]>mid){
c = b;
}else {
c = Math.max(a+1,b);
}
a = b;
b = c;
}
if (c>=k){
r = mid;
}else {
l = mid+1;
}
}
return l;
}
}
|



