对角线上的质数

示例 1:
1
2
3
| 输入:nums = [[1,2,3],[5,6,7],[9,10,11]]
输出:11
解释:数字 1、3、6、9 和 11 是所有 "位于至少一条对角线上" 的数字。由于 11 是最大的质数,故返回 11 。
|
示例 2:
1
2
3
| 输入:nums = [[1,2,3],[5,17,7],[9,11,10]]
输出:17
解释:数字 1、3、9、10 和 17 是所有满足"位于至少一条对角线上"的数字。由于 17 是最大的质数,故返回 17 。
|
代码为:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| class Solution {
public int diagonalPrime(int[][] nums) {
int max = 0;
for (int i = 0;i<nums.length;i++){
max = Math.max(max,isOk(nums[i][i]));
max = Math.max(max,isOk(nums[i][nums.length-1-i]));
}
return max;
}
public int isOk(int n){
if(n<=1) return 0;
for (int i = 2;i*i<=n;i++){
if (n%i==0) return 0;
}
return n;
}
}
|
等值距离和
示例 1:
1
2
3
4
5
6
7
8
| 输入:nums =
输出:
解释:
i = 0 ,nums == nums 且 nums == nums 。因此,arr = |0 - 2| + |0 - 3| = 5 。
i = 1 ,arr = 0 因为不存在值等于 3 的其他下标。
i = 2 ,nums == nums 且 nums == nums 。因此,arr = |2 - 0| + |2 - 3| = 3 。
i = 3 ,nums == nums 且 nums == nums 。因此,arr = |3 - 0| + |3 - 2| = 4 。
i = 4 ,arr = 0 因为不存在值等于 2 的其他下标。
|
示例 2:
1
2
3
| 输入:nums = [0,5,3]
输出:[0,0,0]
解释:因为 nums 中的元素互不相同,对于所有 i ,都有 arr[i] = 0 。
|
+++++++++++++
思路:这题可以使用前缀和+二分法的方式进行解答
这题的意思就是求每个数的下标到与它想等数的下标距离之和。
例如说:示例1中,值为1的下标为0,与它相等值得下标为2和3,因此就是求0到2和3的距离之和。
在做这道题之前先做一下力扣周赛的2602题,和这题使用相同的方法。
先来看看这道题吧:
示例 1:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| 输入:nums = , queries =
输出:
解释:第一个查询,我们可以执行以下操作:
- 将 nums 减小 2 次,nums = 。
- 将 nums 减小 5 次,nums = 。
- 将 nums 减小 7 次,nums = 。
第一个查询的总操作次数为 2 + 5 + 7 = 14 。
第二个查询,我们可以执行以下操作:
- 将 nums 增大 2 次,nums = 。
- 将 nums 增大 4 次,nums = 。
- 将 nums 减小 1 次,nums = 。
- 将 nums 减小 3 次,nums = 。
第二个查询的总操作次数为 2 + 4 + 1 + 3 = 10
|
示例 2:
1
2
3
| 输入:nums = [2,9,6,3], queries = [10]
输出:[20]
解释:我们可以将数组中所有元素都增大到 10 ,总操作次数为 8 + 1 + 4 + 7 = 20
|
这个就是求queriise数组中的数到nums数组中每一个数的距离和。
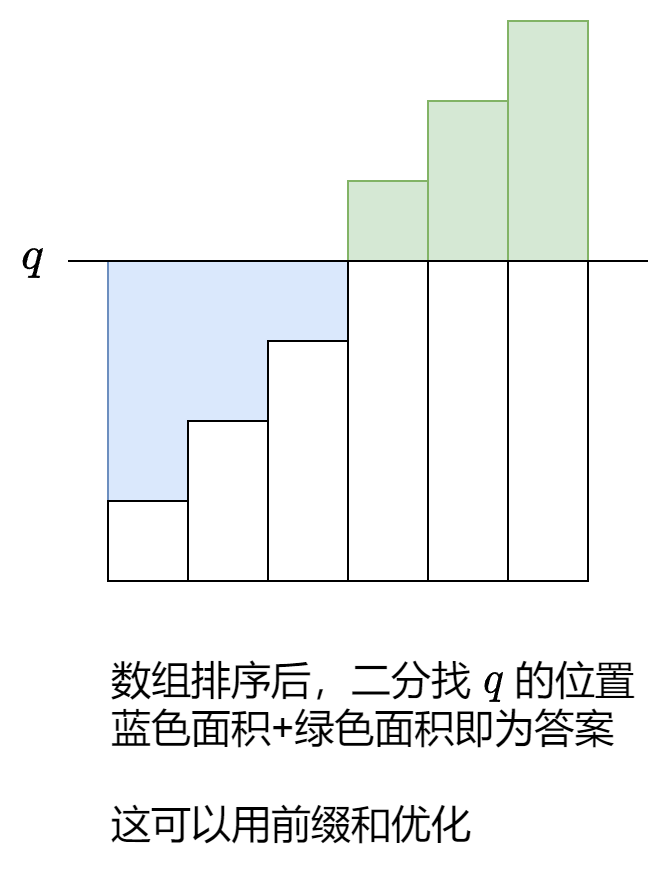
首先将num排序,也就是图中的柱状体,图中的q就是querise中的数。那么距离就等于蓝色面积+绿色面积。为了简化计算过程,加入了前缀和来方便计算面积。
代码为:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
| class Solution {
public List<Long> minOperations(int[] nums, int[] queries) {
Arrays.sort(nums);
int n = nums.length;
long sum[] = new long[n+1];
for (int i = 1;i<n+1;i++){
sum[i] = sum[i-1] + nums[i-1];
}
List<Long> list = new ArrayList<>();
for (int i = 0;i<queries.length;i++){
int a = queries[i];
int p = search(nums,a);
long left = (long)a*p - sum[p];
long right = sum[n]-sum[p]-(n-p)*(long)a;
list.add(left+right);
}
return list;
}
public int search(int nums[],int a){
int l =0;
int r = nums.length;
while (l<r){
int mid = (l+r)>>1;
if (nums[mid]>=a){
r = mid;
}else {
l = mid +1;
}
}
return r;
}
}
|
以上这题会做了后,那这道题的代码为:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| class Solution {
public long[] distance(int[] nums) {
HashMap<Integer,List<Integer>> map = new HashMap<>();
int n = nums.length;
for (int i = 0;i<n;i++){
map.computeIfAbsent(nums[i],(k)->new ArrayList<>()).add(i);
}
long res[] = new long[n];
for (List<Integer> list:map.values()){
int size = list.size();
long sum[] = new long[size+1];
for (int i = 1;i<=size;i++){
sum[i] = sum[i-1] + list.get(i-1);
}
for (int i = 0;i<size;i++){
int a = list.get(i);
long left = i*(long)a-sum[i];
long right = sum[size]-sum[i]-(long)a*(size-i);
res[a] = left + right;
}
}
return res;
}
}
|
最小化数对的最大差值
示例 1:
1
2
3
4
| 输入:nums = , p = 2
输出:1
解释:第一个下标对选择 1 和 4 ,第二个下标对选择 2 和 5 。
最大差值为 max(|nums - nums|, |nums - nums|) = max(0, 1) = 1 。所以我们返回 1
|
示例 2:
1
2
3
| 输入:nums = [4,2,1,2], p = 1
输出:0
解释:选择下标 1 和 3 构成下标对。差值为 |2 - 2| = 0 ,这是最大差值的最小值。
|
+++++++++++
思路:
看到「最大化最小值」或者「最小化最大值」就要想到二分答案,这是一个固定的套路。
这题可以参考打家劫舍 IV
下面先看打家劫舍这道题怎么做:
示例 1:
1
2
3
4
5
6
7
8
9
| 输入:nums = [2,3,5,9], k = 2
输出:5
解释:
小偷窃取至少 2 间房屋,共有 3 种方式:
- 窃取下标 0 和 2 处的房屋,窃取能力为 max(nums[0], nums[2]) = 5 。
- 窃取下标 0 和 3 处的房屋,窃取能力为 max(nums[0], nums[3]) = 9 。
- 窃取下标 1 和 3 处的房屋,窃取能力为 max(nums[1], nums[3]) = 9 。
因此,返回 min(5, 9, 9) = 5 。
|
示例 2:
1
2
3
| 输入:nums = [2,7,9,3,1], k = 2
输出:2
解释:共有 7 种窃取方式。窃取能力最小的情况所对应的方式是窃取下标 0 和 4 处的房屋。返回 max(nums[0], nums[4]) = 2 。
|
思路:二分法 + dp
二分法:通过二分法寻找可能出现的结果,保证所偷取的房间数>=k。
dp:计算通过二分法猜想的结果,可以偷取多少个房间。
代码为:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| class Solution {
public int minCapability(int[] nums, int k) {
int n = nums.length;
int l = 1;
int r = Arrays.stream(nums).max().getAsInt();
int dp[] = new int[n+1];
while (l<r){
int mid = (l+r)>>1;
if (nums[0]<=mid) {
dp[1] = 1;
}else dp[1] = 0;
for (int i = 2;i<=nums.length;i++){
if (nums[i-1]>mid){
dp[i] = dp[i-1];
}else {
dp[i] = Math.max(dp[i-2]+1,dp[i-1]);
}
}
if (dp[n]>=k){
r = mid;
}else {
l = mid+1;
}
}
return r;
}
}
|
优化:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| class Solution {
public static int minCapability(int[] nums, int k) {
int n = nums.length;
int l = 1;
int r = Arrays.stream(nums).max().getAsInt();
while (l<r){
int mid = (l+r)>>1;
int a = 0;
int b = nums[0]<=mid?1:0;
int c = 0;
for (int i = 2;i<=nums.length;i++){
if (nums[i-1]>mid){
c = b;
}else {
c = Math.max(a+1,b);
}
a = b;
b = c;
}
if (c>=k){
r = mid;
}else {
l = mid+1;
}
}
return l;
}
}
|
这道题与上一道题的解法相同:
代码为:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| class Solution {
public int minimizeMax(int[] nums, int p) {
Arrays.sort(nums);
int n = nums.length;
int l = 0;
int r = nums[n-1];
int dp[] = new int[n+1];
while (l<r){
int mid =(l+r)>>1;
for (int i = 0;i<nums.length-1;i++){
if (nums[i+1]-nums[i]<=mid){
dp[i+2] = dp[i] + 1;
}else {
dp[i+2] = dp[i+1];
}
}
if (dp[n]>=p){
r = mid;
}else {
l = mid + 1;
}
}
return l;
}
}
|
以上动态规划也可以优化为贪心做法:

优化后的代码为:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| class Solution {
public int minimizeMax(int[] nums, int p) {
Arrays.sort(nums);
int n = nums.length;
int l = 0;
int r = nums[n-1];
while (l<r){
int mid =(l+r)>>1;
int count = 0;
for (int i = 0;i<nums.length-1;i++){
if (nums[i+1]-nums[i]<=mid){
count++;
i++;
}
}
if (count>=p){
r = mid;
}else {
l = mid + 1;
}
}
return l;
}
}
|






