第六次-324场周赛

算法1：统计相似字符串对的数目（6265）

给你一个下标从 0 开始的字符串数组 words 。

如果两个字符串由相同的字符组成，则认为这两个字符串 相似 。

• 例如，"abca" 和 "cba" 相似，因为它们都由字符 'a'、'b'、'c' 组成。
• 然而，"abacba" 和 "bcfd" 不相似，因为它们不是相同字符组成的。
  请你找出满足字符串 words[i] 和 words[j] 相似的下标对 (i, j) ，并返回下标对的数目，其中 0 <= i < j <= word.length - 1 。

示例 1：

输入：words = ["aba","aabb","abcd","bac","aabc"]
输出：2
解释：共有 2 对满足条件：
- i = 0 且 j = 1 ：words[0] 和 words[1] 只由字符 'a' 和 'b' 组成。 
- i = 3 且 j = 4 ：words[3] 和 words[4] 只由字符 'a'、'b' 和 'c' 。 

示例 2：

输入：words = ["aabb","ab","ba"]
输出：3
解释：共有 3 对满足条件：
- i = 0 且 j = 1 ：words[0] 和 words[1] 只由字符 'a' 和 'b' 组成。 
- i = 0 且 j = 2 ：words[0] 和 words[2] 只由字符 'a' 和 'b' 组成。 
- i = 1 且 j = 2 ：words[1] 和 words[2] 只由字符 'a' 和 'b' 组成。 

示例 3：

输入：words = ["nba","cba","dba"]
输出：0
解释：不存在满足条件的下标对，返回 0 。

+++++++++++

简单题

思路：暴力，使用set来统计每个字符串的字符，通过对比两个set来判断是否相等

代码为：

class Solution {
    public static int similarPairs(String[] words) {
        int res = 0;
        boolean f = true;
        for (int i = 0;i<words.length-1;i++){
            String s = words[i];
            HashSet<Character> set = new HashSet<>();
            for (int a = 0;a<s.length();a++){
                set.add(s.charAt(a));
            }
            for (int j = i+1;j<words.length;j++){
                String s1 = words[j];
                HashSet<Character> set1 = new HashSet<>();
                for (int b = 0;b<s1.length();b++){
                    set1.add(s1.charAt(b));
                }
                if (set1.equals(set)) res++;
            }
        }
        return res;
    }
}

算法2：使用质因数之和替换后可以取到得最小值（2507）

给你一个正整数 n 。

请你将 n 的值替换为 n 的 质因数 之和，重复这一过程。

注意，如果 n 能够被某个质因数多次整除，则在求和时，应当包含这个质因数同样次数。
返回 n 可以取到的最小值。

示例 1：

输入：n = 15
输出：5
解释：最开始，n = 15 。
15 = 3 * 5 ，所以 n 替换为 3 + 5 = 8 。
8 = 2 * 2 * 2 ，所以 n 替换为 2 + 2 + 2 = 6 。
6 = 2 * 3 ，所以 n 替换为 2 + 3 = 5 。
5 是 n 可以取到的最小值。

示例 2：

输入：n = 3
输出：3
解释：最开始，n = 3 。
3 是 n 可以取到的最小值。

+++++++++++++

中等题

思路：对n进行拆分，再对剩下得进行拆分，在这个过程中对结果进行相加，如果最后得结果是质数则直接返回，如果不是质数则再次进行整除拆分。

分解质因数：sum为质因数i的和，n不断分解出质因数i，并更新n/=i，直到n不可再分（质因数为自身和1），此时sum就是初始n的所有质因数之和

代码为;

class Solution {
    public static int smallestValue(int n) {
        if(n == 4){return 4;}
        if (isPrime(n)) return n;
        while (!isPrime(n)){
            int sum = 0;
            int i = 2;
            while (n>1){
                if (n % i==0) {
                    sum += i;
                    n /= i;
                }else i++;
            }
            n = sum;
        }
        return n;
    }
    //判断是否是质数
    public static boolean isPrime(int x){
        if (x<3) return true;
        for (int i = 2;i<x;i++){
            if (x%i==0) return false;
        }
        return true;
    }
}

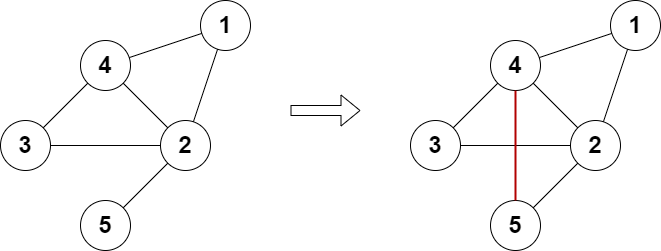
算法3：添加边使得所有节点的度都为偶数（6267）

给你一个有 n 个节点的 无向 图，节点编号为 1 到 n 。再给你整数 n 和一个二维整数数组 edges ，其中 edges[i] = [ai, bi] 表示节点 ai 和 bi 之间有一条边。图不一定连通。

你可以给图中添加 至多 两条额外的边（也可以一条边都不添加），使得图中没有重边也没有自环。

如果添加额外的边后，可以使得图中所有点的度数都是偶数，返回 true ，否则返回 false 。

点的度数是连接一个点的边的数目。

示例 1：

输入：n = 5, edges = [[1,2],[2,3],[3,4],[4,2],[1,4],[2,5]]
输出：true
解释：上图展示了添加一条边的合法方案。
最终图中每个节点都连接偶数条边。

示例 2：

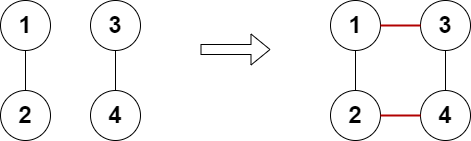
输入：n = 4, edges = [[1,2],[3,4]]
输出：true
解释：上图展示了添加两条边的合法方案。

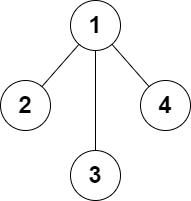
示例 3：

输入：n = 4, edges = [[1,2],[1,3],[1,4]]
输出：false
解释：无法添加至多 2 条边得到一个符合要求的图。

++++++++++++

困难题

思路：

（1）首先构建图

（2）保留度数为奇数的节点，并计算奇数节点的个数

（3）如果度数为奇数的节点个数为奇数时，无论怎么连接，最后的节点度数都不会为偶数。（因为增加一条边会导致两个节点的度数发生变化）。如果度数为奇数的节点个数大于4时，则不成立

（4）之后对于偶数分情况讨论，分别为0，2，4

• 当个数为0时，直接返回true，已经满足题意得要求。

• 当个数为2时，节点分别为x和y

  • 如果节点x和节点y之间没有连线，则直接返回true，将x和y连接即可。
  • 如果有连线，则遍历其他偶数度得节点，如果其中某个节点与x和y都没有连接，则返回true，进行连接即可。

• 当个数为4时，节点分别为a,b,c,d

  • 如果 a 和 b 以及 c 和 d 之间没有边，那么连边之后就符合要求了。
  • 如果 a 和 c 以及 b 和 d 之间没有边，那么连边之后就符合要求了。
  • 如果 a 和 d 以及 b 和 c 之间没有边，那么连边之后就符合要求了。

  其他情况不满足。

代码为

class Solution {
    public static boolean isPossible(int n, List<List<Integer>> edges) {
        List<Integer> list[] = new ArrayList[n+1];
        for (int i =1 ;i<=n;i++){
            list[i] = new ArrayList<>();
        }
        //建立图
        for (List<Integer> l:edges){
            int x = l.get(0);
            int y = l.get(1);
            list[x].add(y);
            list[y].add(x);
        }
        //度为奇数得节点
        List<Integer> oddList = new ArrayList<>();
        for (int i = 1;i<=n;i++){
            if ((list[i].size())%2==1){
                oddList.add(i);
            }
        }
        int size = oddList.size();
        if (size==0) return true;
        if (size==1 || size==3 || size>4) return false;
        if (size==2){
            int a = oddList.get(0);
            int b = oddList.get(1);
            if (!isConnect(a,b,list)) return true;
            for (int i = 1;i<=n;i++){
                if (i==a || i==b) continue;
                if (!isConnect(i,a,list) && !isConnect(i,b,list)) return true;
            }
            return false;
        }
        if (size==4){
            int a = oddList.get(0);
            int b = oddList.get(1);
            int c = oddList.get(2);
            int d = oddList.get(3);
            if (!isConnect(a,b,list) && !isConnect(c,d,list)) return true;
            if (!isConnect(a,c,list) && !isConnect(b,d,list)) return true;
            if (!isConnect(a,d,list) && !isConnect(b,c,list)) return true;
            return false;
        }
        return false;
    }
    //判断是否有连边
    public static boolean isConnect(int x,int y,List<Integer> list[]){
        return list[x].contains(y);
    }
}

算法4：查询树中环的长度

给你一个整数 n ，表示你有一棵含有 2n - 1 个节点的 完全二叉树 。根节点的编号是 1 ，树中编号在[1, 2n - 1 - 1] 之间，编号为 val 的节点都有两个子节点，满足：

• 左子节点的编号为 2 * val

• 右子节点的编号为 2 * val + 1

  给你一个长度为 m 的查询数组 queries ，它是一个二维整数数组，其中 queries[i] = [ai, bi] 。对于每个查询，求出以下问题的解：

1.在节点编号为 `ai` 和 `bi` 之间添加一条边。
2.求出图中环的长度。
3.删除节点编号为 `ai` 和 `bi` 之间新添加的边。

注意：

• 环 是开始和结束于同一节点的一条路径，路径中每条边都只会被访问一次。
• 环的长度是环中边的数目。
• 在树中添加额外的边后，两个点之间可能会有多条边。
  请你返回一个长度为 m 的数组 answer ，其中 answer[i] 是第 i 个查询的结果。

示例 1：

输入：n = 3, queries = [[5,3],[4,7],[2,3]]
输出：[4,5,3]
解释：上图是一棵有 23 - 1 个节点的树。红色节点表示添加额外边后形成环的节点。
- 在节点 3 和节点 5 之间添加边后，环为 [5,2,1,3] ，所以第一个查询的结果是 4 。删掉添加的边后处理下一个查询。
- 在节点 4 和节点 7 之间添加边后，环为 [4,2,1,3,7] ，所以第二个查询的结果是 5 。删掉添加的边后处理下一个查询。
- 在节点 2 和节点 3 之间添加边后，环为 [2,1,3] ，所以第三个查询的结果是 3 。删掉添加的边。

示例 2：

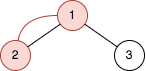
输入：n = 2, queries = [[1,2]]
输出：[2]
解释：上图是一棵有 22 - 1 个节点的树。红色节点表示添加额外边后形成环的节点。
- 在节点 1 和节点 2 之间添加边后，环为 [2,1] ，所以第一个查询的结果是 2 。删掉添加的边。

++++++++++++++

困难题

思路：找到想要询问的两个点的最近公共祖先。

环可以看成是从 a出发往上走，在某个位置「拐弯」，往下走到 b。

这个拐弯的地方就是 a 和 b的最近公共祖先。

设 LCA 为 a 和 b 的最近公共祖先，那么环长等于LCA 到 a 的距离加LCA 到 b 的距离加一。

如何找 LCA？

注意到在完全二叉树中，深度越深的点，其编号必定大于上一层的节点编号，根据这个性质，我们可以不断循环，每次循环比较 a 和 b 的大小：

• 如果 a>b，则 a 的深度大于等于 b的深度，那么把 a移动到其父节点，即 a=a/2；
• 如果 a<b，则 a 的深度小于等于 b 的深度，那么把 bb 移动到其父节点，即 b=b/2；
• 如果 a=b，则找到了LCA，退出循环。

也就是一点点向上寻找，找到最近的公共祖先，找的过程中记录长度。

代码为

class Solution {
    public int[] cycleLengthQueries(int n, int[][] queries) {
        int res[] = new int[queries.length];
        int index = 0;
        int f = 0;
        for (int i = 0;i<queries.length;i++){
            int a = queries[i][0];
            int b = queries[i][1];
            f = 0;
            while (a!=b) {
                if (a > b) a = a / 2;
                else  b = b / 2;
                f++;
            }
            res[index++] = f+1;
        }
        return res;
    }
}