第五次-323场周赛

算法1：删除每行中的最大值（2500）

给你一个 m x n 大小的矩阵 grid ，由若干正整数组成。

执行下述操作，直到 grid 变为空矩阵：

  • 从每一行删除值最大的元素。如果存在多个这样的值，删除其中任何一个。
  • 将删除元素中的最大值与答案相加。
    注意 每执行一次操作，矩阵中列的数据就会减 1 。

返回执行上述操作后的答案。

示例 1：

img

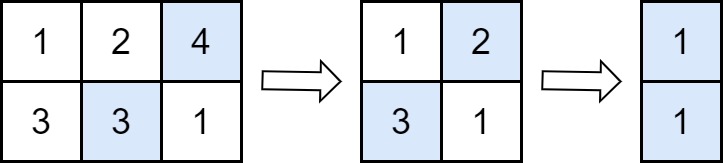
1
2
3
4
5
6
7
输入：grid = [[1,2,4],[3,3,1]]
输出：8
解释：上图展示在每一步中需要移除的值。
- 在第一步操作中，从第一行删除 4 ，从第二行删除 3（注意，有两个单元格中的值为 3 ，我们可以删除任一）。在答案上加 4 。
- 在第二步操作中，从第一行删除 2 ，从第二行删除 3 。在答案上加 3 。
- 在第三步操作中，从第一行删除 1 ，从第二行删除 1 。在答案上加 1 。
最终，答案 = 4 + 3 + 1 = 8 。

示例 2：

img

1
2
3
4
5
输入：grid = [[10]]
输出：10
解释：上图展示在每一步中需要移除的值。
- 在第一步操作中，从第一行删除 10 。在答案上加 10 。
最终，答案 = 10 。

++++++++++++++

简单题

思路1：暴力做法，循环遍历每一行中的最大值，再拿出每一行中最大值的最大数。使用一个辅助变量来验证该数是否之前已经取过。

代码为：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
    public static int deleteGreatestValue(int[][] grid) {
        int m = grid.length;
        int n = grid[0].length;
        if (m==0 && n==0) return grid[0][0];
        int max;
        int max_ans = 0;
        int res = 0;
        int a = 0,b = 0;
        boolean used[][] = new boolean[m][n];
        int y = n;
        while (y-->=0) {
            max_ans = 0;
            for (int i = 0; i < m; i++) {
                max = 0;
                for (int j = 0; j < n; j++) {
                   if (!used[i][j] && grid[i][j]>=max) {
                       max = grid[i][j];
                       a = i;
                       b = j;
                   }
                }
                used[a][b] = true;
                max_ans = Math.max(max,max_ans);
            }
            res+=max_ans;
        }
        return res;
    }
}

思路2：很巧妙。我咋就没想到呢~~。将数组的每一行进行排序，相加每一列的最大的数就是结果

代码为

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    public static int deleteGreatestValue(int[][] grid) {
        for (int i = 0;i<grid.length;i++){
            Arrays.sort(grid[i]);
        }
        int max = 0;
        int res = 0;
        for (int i = 0;i<grid[0].length;i++){
            max = 0;
            for (int j = 0;j<grid.length;j++){
                max = Math.max(max,grid[j][i]);
            }
            res+=max;
        }
        return res;
    }
}

算法2：数组中最长的方波（2501）

给你一个整数数组 nums 。如果 nums 的子序列满足下述条件，则认为该子序列是一个 方波 ：

  • 子序列的长度至少为 2 ，并且
  • 将子序列从小到大排序 之后 ，除第一个元素外，每个元素都是前一个元素的 平方 。
    返回 nums 中 最长方波 的长度，如果不存在 方波 则返回 -1 。

子序列 也是一个数组，可以由另一个数组删除一些或不删除元素且不改变剩余元素的顺序得到。

示例 1 ：

1
2
3
4
5
6
7
输入：nums = [4,3,6,16,8,2]
输出：3
解释：选出子序列 [4,16,2] 。排序后，得到 [2,4,16] 。
- 4 = 2 * 2.
- 16 = 4 * 4.
因此，[4,16,2] 是一个方波.
可以证明长度为 4 的子序列都不是方波。

示例 2 ：

1
2
3
输入：nums = [2,3,5,6,7]
输出：-1
解释：nums 不存在方波，所以返回 -1 。

++++++++++++

中等题

思路：先对数组排序，再进行遍历搜索，在对每一个元素搜索的时候使用二分法进行查找。

代码为：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
    public int longestSquareStreak(int[] nums) {
        Arrays.sort(nums);
        int max = 0;
        for (int i = 0;i<nums.length;i++){
            int count = 1;
            int a = nums[i];
            //优化
            if (a*a>nums[nums.length-1]) break;
            while (binSearch(nums,a*a)){
                count++;
                a= a*a;
            }
            max = Math.max(count,max);
        }
        if (max<=1) return -1;
        else return max;
    }
    //二分法查找
    public boolean binSearch(int nums[],int x){
        int l = 0;
        int r = nums.length-1;
        while (l<r){
            int mid = (l+r)/2;
            if (nums[mid]<x) l = mid+1;
            else r = mid;
        }
        return nums[l]==x;
    }
}

也可以使用封装好的二分法进行查找，代码为：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    public int longestSquareStreak(int[] nums) {
        Arrays.sort(nums);
        int max = 0;
        for (int i = 0;i<nums.length;i++){
            int count = 1;
            if (nums[i]*nums[i]>nums[nums.length-1]) break;
            int idx = i;
            while (idx>=0){
                //封装好的二分查找法
                idx = Arrays.binarySearch(nums,nums[idx]*nums[idx]);
                if (idx >= 0) ++count;
            }
            max = Math.max(count,max);
        }
        if (max<=1) return -1;
        else return max;
    }
}

算法3：设计内存分配器（2502）

给你一个整数 n ，表示下标从 0 开始的内存数组的大小。所有内存单元开始都是空闲的。

请你设计一个具备以下功能的内存分配器：

  1. 分配 一块大小为 size 的连续空闲内存单元并赋 id mID 。
  2. 释放 给定 id mID 对应的所有内存单元。

注意：

  • 多个块可以被分配到同一个 mID 。
  • 你必须释放 mID 对应的所有内存单元，即便这些内存单元被分配在不同的块中。

实现 Allocator 类：

  • Allocator(int n) 使用一个大小为 n 的内存数组初始化 Allocator 对象。
  • int allocate(int size, int mID) 找出大小为 size 个连续空闲内存单元且位于 最左侧 的块，分配并赋 id mID 。返回块的第一个下标。如果不存在这样的块，返回 -1 。
  • int free(int mID) 释放 id mID 对应的所有内存单元。返回释放的内存单元数目。

示例：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
输入
["Allocator", "allocate", "allocate", "allocate", "free", "allocate", "allocate", "allocate", "free", "allocate", "free"]
[[10], [1, 1], [1, 2], [1, 3], [2], [3, 4], [1, 1], [1, 1], [1], [10, 2], [7]]
输出
[null, 0, 1, 2, 1, 3, 1, 6, 3, -1, 0]

解释
Allocator loc = new Allocator(10); // 初始化一个大小为 10 的内存数组，所有内存单元都是空闲的。
loc.allocate(1, 1); // 最左侧的块的第一个下标是 0 。内存数组变为 [1, , , , , , , , , ]。返回 0 。
loc.allocate(1, 2); // 最左侧的块的第一个下标是 1 。内存数组变为 [1,2, , , , , , , , ]。返回 1 。
loc.allocate(1, 3); // 最左侧的块的第一个下标是 2 。内存数组变为 [1,2,3, , , , , , , ]。返回 2 。
loc.free(2); // 释放 mID 为 2 的所有内存单元。内存数组变为 [1, ,3, , , , , , , ] 。返回 1 ，因为只有 1 个 mID 为 2 的内存单元。
loc.allocate(3, 4); // 最左侧的块的第一个下标是 3 。内存数组变为 [1, ,3,4,4,4, , , , ]。返回 3 。
loc.allocate(1, 1); // 最左侧的块的第一个下标是 1 。内存数组变为 [1,1,3,4,4,4, , , , ]。返回 1 。
loc.allocate(1, 1); // 最左侧的块的第一个下标是 6 。内存数组变为 [1,1,3,4,4,4,1, , , ]。返回 6 。
loc.free(1); // 释放 mID 为 1 的所有内存单元。内存数组变为 [ , ,3,4,4,4, , , , ] 。返回 3 ，因为有 3 个 mID 为 1 的内存单元。
loc.allocate(10, 2); // 无法找出长度为 10 个连续空闲内存单元的空闲块，所有返回 -1 。
loc.free(7); // 释放 mID 为 7 的所有内存单元。内存数组保持原状，因为不存在 mID 为 7 的内存单元。返回 0 。

++++++++++++++++

中等题

思路：暴力

代码为

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
class Allocator {

    int allocator[];

    public Allocator(int n) {
        allocator = new int[n];
    }

    public int allocate(int size, int mID) {
        for (int i =0;i<allocator.length;i++){
            int j = i;
            while (j<allocator.length && allocator[j]==0 && j-i<size){
                j++;
            }
            if (j-i==size){
                for (int k = i;k<j;k++) allocator[k] = mID;
                return i;
            }
            i = j;
        }
        return -1;
    }

    public int free(int mID) {
        int count = 0;
        for (int i = 0;i<allocator.length;i++){
            if (allocator[i]==mID) {
                allocator[i] = 0;
                count++;
            }
        }
        return count;
    }
}

/**
 * Your Allocator object will be instantiated and called as such:
 * Allocator obj = new Allocator(n);
 * int param_1 = obj.allocate(size,mID);
 * int param_2 = obj.free(mID);
 */
力扣周赛
第五次-323场周赛
http://example.com/2022/12/17/第五次-323场周赛/
作者
zlw
发布于
2022年12月17日
许可协议