算法1:回环句(6253)
句子 是由单个空格分隔的一组单词,且不含前导或尾随空格。
- 例如,
"Hello World"、"HELLO"、"hello world hello world" 都是符合要求的句子。
单词 仅 由大写和小写英文字母组成。且大写和小写字母会视作不同字符。
如果句子满足下述全部条件,则认为它是一个 回环句 :
给你一个字符串 sentence ,请你判断它是不是一个回环句。如果是,返回 true ;否则,返回 false 。
示例 1:
1
2
3
4
5
6
7
8
| 输入:sentence = "leetcode exercises sound delightful"
输出:true
解释:句子中的单词是 ["leetcode", "exercises", "sound", "delightful"] 。
- leetcode 的最后一个字符和 exercises 的第一个字符相等。
- exercises 的最后一个字符和 sound 的第一个字符相等。
- sound 的最后一个字符和 delightful 的第一个字符相等。
- delightful 的最后一个字符和 leetcode 的第一个字符相等。
这个句子是回环句。
|
示例 2:
1
2
3
4
5
| 输入:sentence = "eetcode"
输出:true
解释:句子中的单词是 ["eetcode"] 。
- eetcode 的最后一个字符和 eetcode 的第一个字符相等。
这个句子是回环句。
|
+++++++++++++++++++
简单题
思路:将字符串通过空格分隔,遍历字符串按照要求比较
代码为:
1
2
3
4
5
6
7
8
9
10
11
12
13
| class Solution {
public boolean isCircularSentence(String sentence) {
int len = sentence.length();
if (sentence.charAt(0)!=sentence.charAt(len-1)) return false;
String[] s = sentence.split(" ");
for (int i = 0;i<s.length-1;i++){
String s1 = s[i];
String s2 = s[i+1];
if (s1.charAt(s1.length()-1)!=s2.charAt(0)) return false;
}
return true;
}
}
|
算法2:划分技能点相等的团队(6254)
给你一个正整数数组 skill ,数组长度为 偶数 n ,其中 skill[i] 表示第 i 个玩家的技能点。将所有玩家分成 n / 2 个 2 人团队,使每一个团队的技能点之和 相等 。
团队的 化学反应 等于团队中玩家的技能点 乘积 。
返回所有团队的 化学反应 之和,如果无法使每个团队的技能点之和相等,则返回 -1 。
示例 1:
1
2
3
4
5
| 输入:skill = [3,2,5,1,3,4]
输出:22
解释:
将玩家分成 3 个团队 (1, 5), (2, 4), (3, 3) ,每个团队的技能点之和都是 6 。
所有团队的化学反应之和是 1 * 5 + 2 * 4 + 3 * 3 = 5 + 8 + 9 = 22 。
|
示例 2:
1
2
3
4
5
| 输入:skill = [3,4]
输出:12
解释:
两个玩家形成一个团队,技能点之和是 7 。
团队的化学反应是 3 * 4 = 12 。
|
示例 3:
1
2
3
4
| 输入:skill = [1,1,2,3]
输出:-1
解释:
无法将玩家分成每个团队技能点都相等的若干个 2 人团队。
|
+++++++++++++++++
中等题
自己的思路:使用hash表记录个数
代码为:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| class Solution {
public long dividePlayers(int[] skill) {
Arrays.sort(skill);
if (skill.length==2) return skill[0]*skill[1];
int sum = 0;
for (int i = 0;i<skill.length;i++){
sum+=skill[i];
}
if(sum%(skill.length/2)!=0) return -1;
int ans = sum/(skill.length/2);
HashMap<Integer,Integer> map = new HashMap<>();
for (int i = 0;i<skill.length;i++) map.put(skill[i],map.getOrDefault(skill[i],0)+1);
long res = 0;
int count = 0;
for (int i = 0;i<skill.length/2;i++){
if (skill[i]>ans) return -1;
if (map.containsKey(ans-skill[i]) && map.get(ans-skill[i])!=0){
res+=skill[i]*(ans-skill[i]);
map.put(ans-skill[i],map.get(ans-skill[i])-1);
map.put(skill[i],map.get(skill[i])-1);
count++;
}
}
if(count==skill.length/2) return res;
else return -1;
}
}
|
大佬的思路:首先对数组进行排序,大哥带小弟进行组队,如果最大的数和最小的数不能匹配,那么最大的和一个比最小数更大的数匹配,因此直接返回负数一。否则向里进行遍历。
代码为
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| class Solution {
public static long dividePlayers(int[] skill) {
Arrays.sort(skill);
if (skill.length==2) return skill[0]*skill[1];
long res = 0;
int sum = Arrays.stream(skill).sum();
int a = sum/(skill.length/2);
if (skill[0]+skill[skill.length-1]==a){
res+=skill[0]*skill[skill.length-1];
}else return -1;
for (int i = 1,j = skill.length-2;i<j;i++,j--){
if (skill[i]+skill[j]!=a) return -1;
res+=skill[i]*skill[j];
}
return res;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| class Solution {
public static long dividePlayers(int[] skill) {
Arrays.sort(skill);
if (skill.length==2) return skill[0]*skill[1];
long res = 0;
int sum = skill[0]+skill[skill.length-1];
res+=skill[0]*skill[skill.length-1];
for (int i = 1,j = skill.length-2;i<j;i++,j--){
if (skill[i]+skill[j]!=sum) return -1;
res+=skill[i]*skill[j];
}
return res;
}
}
|
给你一个正整数 n ,表示总共有 n 个城市,城市从 1 到 n 编号。给你一个二维数组 roads ,其中 roads[i] = [ai, bi, distancei] 表示城市 ai 和 bi 之间有一条 双向 道路,道路距离为 distancei 。城市构成的图不一定是连通的。
两个城市之间一条路径的 分数 定义为这条路径中道路的 最小 距离。
城市 1 和城市 n 之间的所有路径的 最小 分数。
注意:
- 一条路径指的是两个城市之间的道路序列。
- 一条路径可以 多次 包含同一条道路,你也可以沿着路径多次到达城市 1 和城市 n 。
- 测试数据保证城市 1 和城市n 之间 至少 有一条路径。
示例 1:
1
2
3
4
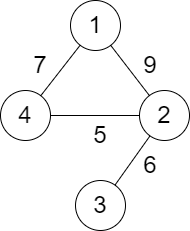
| 输入:n = 4, roads = [[1,2,9],[2,3,6],[2,4,5],[1,4,7]]
输出:5
解释:城市 1 到城市 4 的路径中,分数最小的一条为:1 -> 2 -> 4 。这条路径的分数是 min(9,5) = 5 。
不存在分数更小的路径。
|
示例 2:
1
2
3
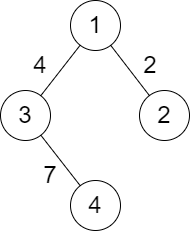
| 输入:n = 4, roads = [[1,2,2],[1,3,4],[3,4,7]]
输出:2
解释:城市 1 到城市 4 分数最小的路径是:1 -> 2 -> 1 -> 3 -> 4 。这条路径的分数是 min(2,2,4,7) = 2 。
|
+++++++++++
中等题
思路:直接使用并查集,在一个连通图中查找最小的边权值。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
| class Solution {
int p[];
public int minScore(int n, int[][] roads) {
p = new int[n+1];
init(n);
int min = Integer.MAX_VALUE;
for (int i = 0;i<roads.length;i++){
int a = roads[i][0];
int b = roads[i][1];
if (find(a)!=find(b)) merge(a,b);
}
for (int i = 0;i<roads.length;i++){
int k = roads[i][0];
if (find(1)==find(k) && roads[i][2]<min) min = roads[i][2];
}
return min;
}
public void merge(int x, int y){
p[find(x)] = find(y);
}
public void init(int n){
for (int i = 0;i<n;i++){
p[i] = i;
}
}
public int find(int x){
if (p[x]!=x){
p[x] = find(p[x]);
}
return p[x];
}
}
|
也可以dfs进行解决
代码为:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| class Solution {
public int minScore(int n, int[][] roads) {
List<int[]> graph[] = new ArrayList[n+1];
for (int i = 1;i<=n;i++){
graph[i] = new ArrayList<>();
}
for (int[] r : roads) {
graph[r[0]].add(new int[]{r[1], r[2]});
graph[r[1]].add(new int[]{r[0], r[2]});
}
boolean used[] = new boolean[n+1];
return dfs(graph,1,used);
}
public int dfs(List<int[]> graph[],int a,boolean used[]){
int min = Integer.MAX_VALUE;
used[a] = true;
for (int to[]:graph[a]){
min = Math.min(min,to[1]);
if (!used[to[0]]){
min = Math.min(min,dfs(graph,to[0],used));
}
}
return min;
}
}
|
算法4:

