第三次-321场周赛

第一题：找出中枢整数（6245）

给你一个正整数 n ，找出满足下述条件的 中枢整数 x ：

• 1 和 x 之间的所有元素之和等于 x 和 n 之间所有元素之和。

  返回中枢整数 x 。如果不存在中枢整数，则返回 -1 。题目保证对于给定的输入，至多存在一个中枢整数。

示例 1：

输入：n = 8
输出：6
解释：6 是中枢整数，因为 1 + 2 + 3 + 4 + 5 + 6 = 6 + 7 + 8 = 21 。

示例 2：

输入：n = 1
输出：1
解释：1 是中枢整数，因为 1 = 1 。

示例 3：

输入：n = 4
输出：-1
解释：可以证明不存在满足题目要求的整数。

+++++++++

简单题

我的思路：通过前缀和，计算数组之间前缀和的差值。

代码为：

class Solution {
    public static int pivotInteger(int n) {
        if(n==1) return 1;
        int arr[] = new int[n+1];
        for (int i = 1;i<=n;i++){
            arr[i] = arr[i-1]+i;
        }
        int i = 1;
        int j = n-1;
        while (i<j){
            int a = arr[i]-arr[0];
            int b = arr[n]-arr[j];
            if (a==b && (j-i==1 || i-j==1)) {
                return i-j==1?i:j;
            }else if (a<b) i++; 
            else j--;
        }
        return -1;
    }
}

其他思路1：通过数学的思想，复杂度只需要O(1)，太妙了！！

因此，通过以上公式，只需要判断数组中遍历的数是否等于上述公式即可

代码为：

public static int pivotInteger(int n) {
        for (int i = 1;i<=n;i++){
            if (i== Math.sqrt(n*(n+1)/2)){
                return i;
            }
        }
        return -1;
    }

其他思路2：遍历数组，分别以数组中的每个数为中心点，计算该数的左右两边的和，判断是否相等。

代码为：

class Solution {
    public static int pivotInteger(int n) {
        int l = 0;
        int r = 0;
        for (int i = 1;i<=n;i++){
            for (int a = 1;a<=i;a++) l+=a;
            for (int b = i;b<=n;b++) r+=b;
            if (l==r) return i;
            l = 0;
            r = 0;
        }
        return -1;
    }
}

第二题：追加字符以获得子序列（6246）

给你两个仅由小写英文字母组成的字符串 s 和 t 。

现在需要通过向 s 末尾追加字符的方式使 t 变成 s 的一个 子序列 ，返回需要追加的最少字符数。

子序列是一个可以由其他字符串删除部分（或不删除）字符但不改变剩下字符顺序得到的字符串。

示例 1：

输入：s = "coaching", t = "coding"
输出：4
解释：向 s 末尾追加字符串 "ding" ，s = "coachingding" 。
现在，t 是 s ("coachingding") 的一个子序列。
可以证明向 s 末尾追加任何 3 个字符都无法使 t 成为 s 的一个子序列。

示例 2：

输入：s = "abcde", t = "a"
输出：0
解释：t 已经是 s ("abcde") 的一个子序列。

示例 3：

输入：s = "z", t = "abcde"
输出：5
解释：向 s 末尾追加字符串 "abcde" ，s = "zabcde" 。
现在，t 是 s ("zabcde") 的一个子序列。 
可以证明向 s 末尾追加任何 4 个字符都无法使 t 成为 s 的一个子序列。

+++++++++++

中等题

思路：很简单，遍历整个s。t有几个没被匹配上就要添加几个

代码

class Solution {
    public static int appendCharacters(String s, String t) {
        int len1 = s.length();
        int len2 = t.length();
        int index  =0;
        for (int i = 0;i<len1 && index<len2;){
            if (s.charAt(i)==t.charAt(index)){
                i++;
                index++;
            }else i++;
        }
        return len2-index;
    }
}

第三题：从链表中移除节点（6247）

给你一个链表的头节点 head 。

对于列表中的每个节点 node ，如果其右侧存在一个具有 严格更大 值的节点，则移除 node 。

返回修改后链表的头节点 head 。

示例 1：

输入：head = [5,2,13,3,8]
输出：[13,8]
解释：需要移除的节点是 5 ，2 和 3 。
- 节点 13 在节点 5 右侧。
- 节点 13 在节点 2 右侧。
- 节点 8 在节点 3 右侧。

示例 2：

输入：head = [1,1,1,1]
输出：[1,1,1,1]
解释：每个节点的值都是 1 ，所以没有需要移除的节点。

++++++++++

中等题

思路：使用一个队列维护，使队列中的元素是降序排列。最后从队列中取元素建立链表。

代码

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode removeNodes(ListNode head) {
        Deque<Integer> deque = new ArrayDeque<>();
        ListNode dummy = new ListNode();
        ListNode p = head;
        while ( p!=null){
            while (!deque.isEmpty() && deque.peekLast()<p.val) deque.removeLast();
            deque.addLast(p.val);
            p = p.next;
        }
        p = dummy;
        while (!deque.isEmpty()){
            ListNode node = new ListNode(deque.removeFirst());
            p.next = node;
            p = p.next;
        }
        return dummy.next;
    }
}

其他思路：递归，从后向前遍历，维护一个最大值（当前节点右边的最大值），如果当前节点小于这个max，则返回当前节点的next，否则返回当前节点。debug可以知道流程

代码

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    private int max;

    public ListNode removeNodes(ListNode head) {
        if(head == null) {
            return null;
        }

        head.next = removeNodes(head.next);
        
        max = Math.max(max, head.val);
        if(head.val < max) {
            return head.next;
        }else {
            return head;
        }
        
    }
}

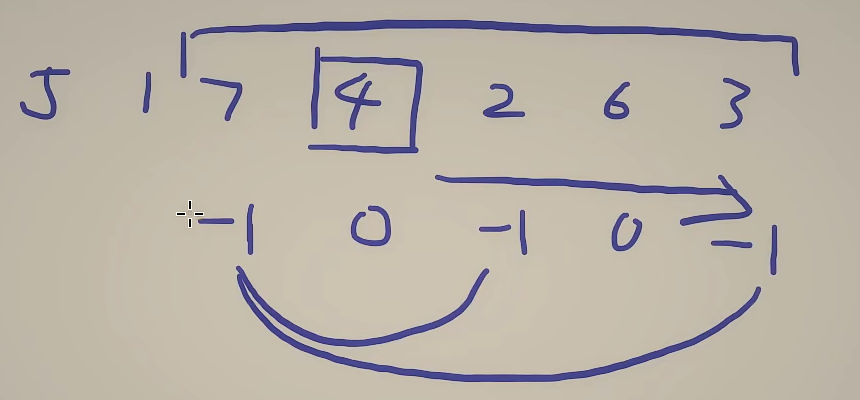
第四题

给你一个长度为 n 的数组 nums ，该数组由从 1 到 n 的 不同 整数组成。另给你一个正整数 k 。

统计并返回 num 中的 中位数 等于 k 的非空子数组的数目。

注意：

• 数组的中位数是按 递增 顺序排列后位于 中间 的那个元素，如果数组长度为偶数，则中位数是位于中间靠 左 的那个元素。
  例如，[2,3,1,4] 的中位数是 2 ，[8,4,3,5,1] 的中位数是 4 。
• 子数组是数组中的一个连续部分。

示例 1：

输入：nums = [3,2,1,4,5], k = 4
输出：3
解释：中位数等于 4 的子数组有：[4]、[4,5] 和 [1,4,5] 。

示例 2：

输入：nums = [2,3,1], k = 3
输出：1
解释：[3] 是唯一一个中位数等于 3 的子数组。

++++++++

困难题，真难呀

思路：展开为一个数学公式：

就是中位数==》在奇数的情况下：小于中位数的个数 = 大于中位数的个数

但该题目求得是子数组，所以不能将数组排序，所以将中位数分为左右两侧来看：

中位数左侧小于+中位数右侧小于 = 中位数左侧大于+中位数右侧大于

在计算得过程中，将左右合为一侧：中位数左侧小于 - 中位数左侧大于 = 中位数右侧大于 - 中位数右侧小于（+1-1 = +1-1）

偶数情况下，小于中位数的个数+1 = 大于中位数的个数。

代码

class Solution {
    public static int countSubarrays(int[] nums, int k) {
        int index = 0;
        for (int i = 0;i<nums.length;i++){
            if (nums[i]==k) index = i;
        }
        Map<Integer,Integer> map = new HashMap<>();
        map.put(0,1);
        int c = 0;
        int res = 0;
        for (int i = index+1;i<nums.length;i++){
            c+=nums[i]<k?-1:1;
            map.put(c,map.getOrDefault(c,0)+1);
        }
        res+=map.get(0)+map.getOrDefault(1,0);
        c = 0;
        for (int i = index-1;i>=0;i--){
            c+=nums[i]<k?1:-1;
            res+=map.getOrDefault(c,0)+map.getOrDefault(c+1,0);
        }
        return res;
    }
}