第一题:数组中不等三元组的数目
给你一个下标从 0 开始的正整数数组 nums 。请你找出并统计满足下述条件的三元组 (i, j, k) 的数目:
0 <= i < j < k < nums.lengthnums[i]、nums[j] 和 nums[k] 两两不同 。
- 换句话说:
nums[i] != nums[j]、nums[i] != nums[k] 且 nums[j] != nums[k] 。
返回满足上述条件三元组的数目。
示例 1:
1
2
3
4
5
6
7
8
9
| 输入:nums = [4,4,2,4,3]
输出:3
解释:下面列出的三元组均满足题目条件:
- (0, 2, 4) 因为 4 != 2 != 3
- (1, 2, 4) 因为 4 != 2 != 3
- (2, 3, 4) 因为 2 != 4 != 3
共计 3 个三元组,返回 3 。
注意 (2, 0, 4) 不是有效的三元组,因为 2 > 0
|
示例 2:
1
2
3
| 输入:nums = [1,1,1,1,1]
输出:0
解释:不存在满足条件的三元组,所以返回 0 。
|
+++++++++++++++
简单题
思路:自己用暴力做的
代码为:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| class Solution {
public static int unequalTriplets(int[] nums) {
int len = nums.length;
int res = 0;
for (int i = 0;i<len;i++){
for (int l = i+1;l<len-1;l++){
int r = l + 1;
while (r<len) {
if (nums[i] == nums[l] || nums[i] == nums[r] || nums[l] == nums[r]) {
r++;
} else {
r++;
res++;
}
}
}
}
return res;
}
}
|
很妙的思路:https://leetcode.cn/problems/number-of-unequal-triplets-in-array/solution/fei-bao-li-zuo-fa-by-endlesscheng-9ekp/
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| class Solution {
public static int unequalTriplets(int[] nums) {
Arrays.sort(nums);
int res = 0;
for (int i = 0,r = 1;r<nums.length;){
if (nums[i]!=nums[r]){
res+=i*(r-i)*(nums.length-r);
i = r;
}else {
r++;
}
}
return res;
}
}
|
第二题:二叉搜索树最近节点查询
给你一个 二叉搜索树 的根节点 root ,和一个由正整数组成、长度为 n 的数组 queries 。
请你找出一个长度为 n 的 二维 答案数组 answer ,其中 answer[i] = [mini, maxi] :
mini 是树中小于等于 queries[i] 的 最大值 。如果不存在这样的值,则使用 -1 代替。maxi 是树中大于等于 queries[i] 的 最小值 。如果不存在这样的值,则使用 -1 代替。
返回数组 answer 。
示例 1 :
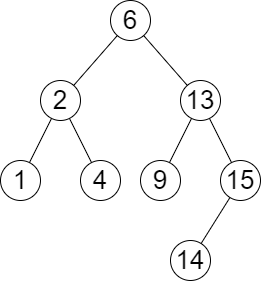
1
2
3
4
5
6
| 输入:root = [6,2,13,1,4,9,15,null,null,null,null,null,null,14], queries = [2,5,16]
输出:[[2,2],[4,6],[15,-1]]
解释:按下面的描述找出并返回查询的答案:
- 树中小于等于 2 的最大值是 2 ,且大于等于 2 的最小值也是 2 。所以第一个查询的答案是 [2,2] 。
- 树中小于等于 5 的最大值是 4 ,且大于等于 5 的最小值是 6 。所以第二个查询的答案是 [4,6] 。
- 树中小于等于 16 的最大值是 15 ,且大于等于 16 的最小值不存在。所以第三个查询的答案是 [15,-1] 。
|
示例 2 :
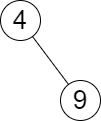
1
2
3
| 输入:root = [4,null,9], queries = [3]
输出:[[-1,4]]
解释:树中不存在小于等于 3 的最大值,且大于等于 3 的最小值是 4 。所以查询的答案是 [-1,4] 。
|
++++++++++++
中等题
思路:首先对树进行遍历,存储到TreeSet中,因为TreeSet中有两个内置方法可以直接获取本题答案。
开始的时候用了二分查找,没有做出来,但感觉应该可以,也许是哪种情况没有考虑对把。我再去试试~~成功了!成功了!
TreeSet中的内置函数floor和ceiling,没有做出来,情况太多,内置函数真的太重要了!!
floor:方法返回在这个集合中小于或者等于给定元素的最大元素,如果不存在这样的元素,返回null.
ceiling:方法返回在这个集合中大于或者等于给定元素的最小元素,如果不存在这样的元素,返回null.
知道这两个方法这题瞬间就变为简单题,hhhh~
代码为:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
|
class Solution {
public List<List<Integer>> closestNodes(TreeNode root, List<Integer> queries) {
TreeSet<Integer> set = new TreeSet<>();
inSearch(root,set);
List<List<Integer>> ans = new ArrayList<>();
for (int q : queries) {
Integer min = set.floor(q);
if (min == null) {
min = -1;
}
Integer max = set.ceiling(q);
if (max == null) {
max = -1;
}
List<Integer> list = new ArrayList<>();
list.add(min);
list.add(max);
ans.add(list);
}
return ans;
}
public static void inSearch(TreeNode root,TreeSet<Integer> set){
if(root!=null){
inSearch(root.left,set);
set.add(root.val);
inSearch(root.right,set);
}
}
}
|
看吧!!!!哈哈哈 我就说可以嘛~
代码为:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
|
class Solution {
List<Integer> list = new ArrayList<>();
public List<List<Integer>> closestNodes(TreeNode root, List<Integer> queries) {
List<List<Integer>> res = new ArrayList<>();
inSearch(root);
int[] arr = list.stream().mapToInt(Integer::intValue).toArray();
for (int i = 0;i<queries.size();i++){
List<Integer> list2 = new ArrayList<>();
int a = queries.get(i);
list2.add(search1(arr,a));
list2.add(search2(arr,a));
res.add(list2);
}
return res;
}
public int search1(int arr[],int a){
int l = 0;
int r = arr.length-1;
while (l<r){
int mid = (l+r+1)/2;
if (arr[mid]<=a){
l = mid;
}else r = mid - 1;
}
return arr[l]<=a?arr[l]:-1;
}
public int search2(int arr[],int a){
int l = 0;
int r = arr.length-1;
while (l<r){
int mid = (l+r)/2;
if (arr[mid]>=a){
r = mid;
}else l = mid+1;
}
return arr[l]>=a?arr[l]:-1;
}
public void inSearch(TreeNode root){
if(root!=null){
if (root.left!=null) inSearch(root.left);
list.add(root.val);
if (root.right!=null) inSearch(root.right);
}
}
}
|
第三题:到达首都的最少油耗
https://leetcode.cn/problems/minimum-fuel-cost-to-report-to-the-capital/
难呀难~~没怎么看懂。
简单写一下把。
给你一棵 n 个节点的树(一个无向、连通、无环图),每个节点表示一个城市,编号从 0 到 n - 1 ,且恰好有 n - 1 条路。0 是首都。给你一个二维整数数组 roads ,其中 roads[i] = [ai, bi] ,表示城市 ai 和 bi 之间有一条 双向路 。
每个城市里有一个代表,他们都要去首都参加一个会议。
每座城市里有一辆车。给你一个整数 seats 表示每辆车里面座位的数目。
城市里的代表可以选择乘坐所在城市的车,或者乘坐其他城市的车。相邻城市之间一辆车的油耗是一升汽油。
请你返回到达首都最少需要多少升汽油。
示例 1:
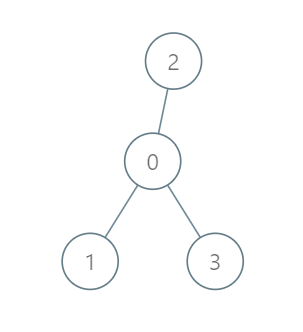
1
2
3
4
5
6
7
| 输入:roads = [[0,1],[0,2],[0,3]], seats = 5
输出:3
解释:
- 代表 1 直接到达首都,消耗 1 升汽油。
- 代表 2 直接到达首都,消耗 1 升汽油。
- 代表 3 直接到达首都,消耗 1 升汽油。
最少消耗 3 升汽油。
|
示例 2:
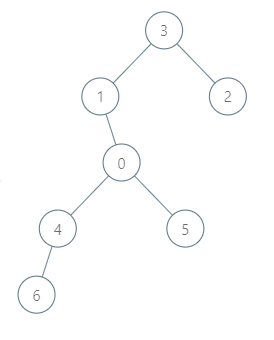
1
2
3
4
5
6
7
8
9
10
11
| 输入:roads = [[3,1],[3,2],[1,0],[0,4],[0,5],[4,6]], seats = 2
输出:7
解释:
- 代表 2 到达城市 3 ,消耗 1 升汽油。
- 代表 2 和代表 3 一起到达城市 1 ,消耗 1 升汽油。
- 代表 2 和代表 3 一起到达首都,消耗 1 升汽油。
- 代表 1 直接到达首都,消耗 1 升汽油。
- 代表 5 直接到达首都,消耗 1 升汽油。
- 代表 6 到达城市 4 ,消耗 1 升汽油。
- 代表 4 和代表 6 一起到达首都,消耗 1 升汽油。
最少消耗 7 升汽油。
|
++++++++++
中等题
思路:将消耗的汽油转化消耗多少辆车,为以0为根节点,分别计算每个子树(每个子树也用同样的方式计算它们的子树–递归操作)所要消耗的车,最后结果相加。
消耗车的数量:每个连边所要经过的人/车的座位数=车的数量,将每个连边加在一起就是总共所需要的数量
代码为:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| class Solution {
long res;
List<List<Integer>> list = new ArrayList<>();
public long minimumFuelCost(int[][] roads, int seats) {
int len = roads.length+1;
for (int i = 0;i<len;i++){
list.add(new ArrayList<>());
}
for (int i = 0;i<roads.length;i++){
list.get(roads[i][0]).add(roads[i][1]);
list.get(roads[i][1]).add(roads[i][0]);
}
dfs(0,-1,seats);
return res;
}
public int dfs(int cur,int father,int seats){
int size = 1;
for (int i:list.get(cur)){
if (i!=father){
size += dfs(i,cur,seats);
}
}
if (cur!=0) res+=(int)Math.ceil((double) size/seats);
return size;
}
}
|
第四题:完美分割的方案数
https://leetcode.cn/problems/number-of-beautiful-partitions/



