第一题(温度转换)
给你一个四舍五入到两位小数的非负浮点数 celsius 来表示温度,以 摄氏度(Celsius)为单位。
你需要将摄氏度转换为 开氏度(Kelvin)和 华氏度(Fahrenheit),并以数组 ans = [kelvin, fahrenheit] 的形式返回结果。
返回数组 ans 。与实际答案误差不超过 10-5 的会视为正确答案。
注意:
开氏度 = 摄氏度 + 273.15华氏度 = 摄氏度 * 1.80 + 32.00
示例 1 :
1
2
3
| 输入:celsius = 36.50
输出:[309.65000,97.70000]
解释:36.50 摄氏度:转换为开氏度是 309.65 ,转换为华氏度是 97.70 。
|
示例 2 :
1
2
3
| 输入:celsius = 122.11
输出:[395.26000,251.79800]
解释:122.11 摄氏度:转换为开氏度是 395.26 ,转换为华氏度是 251.798 。
|
+++++++
简单题
一开始还想复杂了,,哈哈,没有思路可说
1
2
3
4
5
6
7
8
| class Solution {
public double[] convertTemperature(double celsius) {
double res[] = new double[2];
res[0] = celsius+273.15;
res[1] = (celsius*1.8)+32.00;
return res;
}
}
|
第二题(最小公倍数为k的子数组数目)
给你一个整数数组 nums 和一个整数 k ,请你统计并返回 nums 的 子数组 中满足 元素最小公倍数为 k 的子数组数目。
子数组 是数组中一个连续非空的元素序列。
数组的最小公倍数 是可被所有数组元素整除的最小正整数。
示例 1 :
```makefile
输入:nums = [3,6,2,7,1], k = 6
输出:4
解释:以 6 为最小公倍数的子数组是:
- [3,6,2,7,1]
- [3,6,2,7,1]
- [3,6,2,7,1]
- [3,6,2,7,1]
1
2
3
4
5
6
7
|
**示例 2 :**
```makefile
输入:nums = [3], k = 2
输出:0
解释:不存在以 2 为最小公倍数的子数组。
|
++++
中等题
思路:最小公倍数=数的乘积/最大公约数,这题没有做出来的原因是,不会计算最大公约数,,真绝。。还有就是不会算多个数的最小公倍数。
其实多个数的最小公倍数 就是 两个数的最小公倍数的结果再依次和后面的数求最小公倍
求两个数最大公约数的代码:
1
2
3
4
5
6
7
8
9
|
public static int cap(int a,int b) {
while(b!=0) {
int temp = a%b;
a = b;
b =temp;
}
return a;
}
|
代码为:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| class Solution {
public int subarrayLCM(int[] nums, int k) {
int count = 0;
int len = nums.length;
for (int i = 0;i<len;i++){
int t = 1;
for (int j = i;j<len;j++){
t = cap(t,nums[j]);
if(t==k){
count++;
}else if(t>k){
break;
}
}
}
return count;
}
public static int cap(int a,int b) {
int sum = a*b;
while(b!=0) {
int temp = a%b;
a = b;
b =temp;
}
return sum/a;
}
}
|
第三题(逐层排序二叉树所需的最少操作数目)
给你一个 值互不相同 的二叉树的根节点 root 。
在一步操作中,你可以选择 同一层 上任意两个节点,交换这两个节点的值。
返回每一层按 严格递增顺序 排序所需的最少操作数目。
节点的 层数 是该节点和根节点之间的路径的边数。
示例 1 :
```makefile
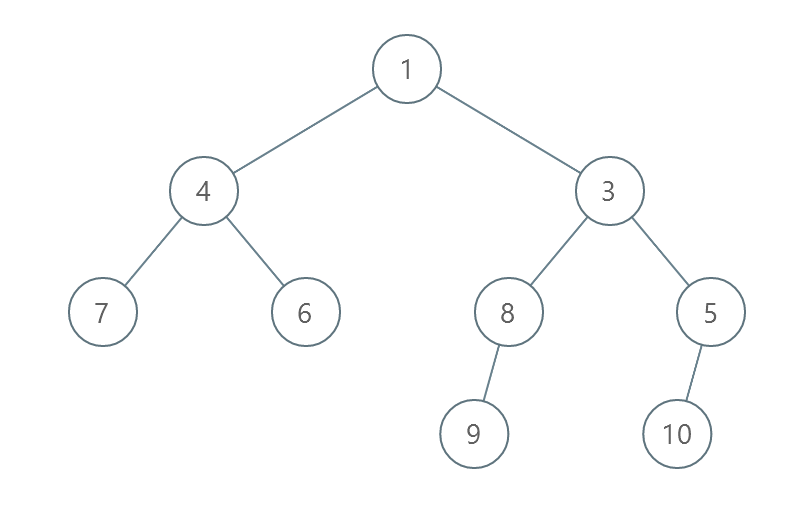
输入:root = [1,4,3,7,6,8,5,null,null,null,null,9,null,10]
输出:3
解释:
- 交换 4 和 3 。第 2 层变为 [3,4] 。
- 交换 7 和 5 。第 3 层变为 [5,6,8,7] 。
- 交换 8 和 7 。第 3 层变为 [5,6,7,8] 。
共计用了 3 步操作,所以返回 3 。
可以证明 3 是需要的最少操作数目。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
**示例 2 :**
- ```makefile
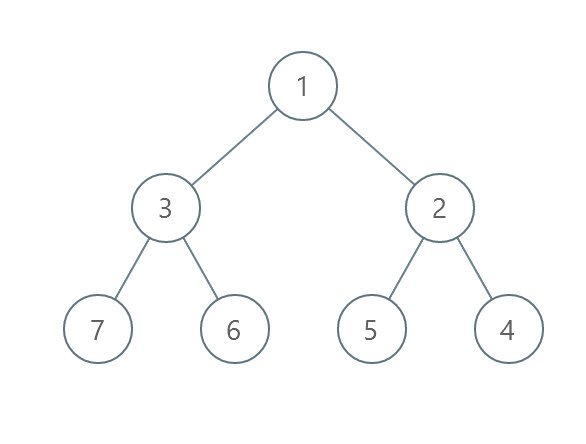
输入:root = [1,3,2,7,6,5,4]
输出:3
解释:
- 交换 3 和 2 。第 2 层变为 [2,3] 。
- 交换 7 和 4 。第 3 层变为 [4,6,5,7] 。
- 交换 6 和 5 。第 3 层变为 [4,5,6,7] 。
共计用了 3 步操作,所以返回 3 。
可以证明 3 是需要的最少操作数目。
|
+++++++++++++++++++++
中等题
思路:层序遍历,将每层的数据存储到链表中,分别对每层的链表进行排序,在排序的过程中,计算交换的位置。
代码为:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
|
class Solution {
public int minimumOperations(TreeNode root) {
int count = 0;
Queue<TreeNode> queue = new LinkedList<>();
List<Integer> list = new ArrayList<>();
if (root!=null) queue.add(root);
while (!queue.isEmpty()){
int size = queue.size();
for (int i = 0;i<size;i++){
TreeNode node = queue.remove();
if (node.left!=null){
queue.add(node.left);
list.add(node.left.val);
}
if (node.right!=null){
queue.add(node.right);
list.add(node.right.val);
}
}
if (list.size()==2) {
if (list.get(0)>list.get(1)) count++;
}
else if (list.size()>1){
count+=selectSort(list.stream().mapToInt(Integer::intValue).toArray());
}
list.clear();
}
return count;
}
public int selectSort(int arr[]){
int count = 0;
int n = arr.length;
int min;
int t = 0;
for (int j = 0;j<n;j++) {
min = arr[j];
t = j;
for (int i = j+1; i < n; i++) {
if (arr[i] < min) {
min = arr[i];
t = i;
}
}
if (t!=j){
int m = arr[j];
arr[j] = arr[t];
arr[t] = m;
count++;
}
}
return count;
}
}
|
第四题(不重叠回文子字符串的最大数目)
给你一个字符串 s 和一个 正 整数 k 。
从字符串 s 中选出一组满足下述条件且 不重叠 的子字符串:
每个子字符串的长度 至少 为 k 。
每个子字符串是一个 回文串 。
返回最优方案中能选择的子字符串的 最大 数目。
子字符串 是字符串中一个连续的字符序列。
示例 1 :
1
2
3
4
| 输入:s = "abaccdbbd", k = 3
输出:2
解释:可以选择 s = "abaccdbbd" 中斜体加粗的子字符串。"aba" 和 "dbbd" 都是回文,且长度至少为 k = 3 。
可以证明,无法选出两个以上的有效子字符串
|
示例 2 :
1
2
3
| 输入:s = "adbcda", k = 2
输出:0
解释:字符串中不存在长度至少为 2 的回文子字符串。
|
++++++++++++
困难题
思路:两次动态规划,第一次动态规划算出dp[i][j]:位置i到j的子字符串是否是回文字符串。第二次计算出dp2[i]:前i个字符满足条件的最大回文串的数量。。
其实第二个动态规划有点没搞懂。等过段时间再来看看。。。希望我不会忘。。。
代码为:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| class Solution {
public int maxPalindromes(String S, int k) {
boolean[][] dp = new boolean[S.length()][S.length()];
for (int i = 0;i<S.length();i++){
dp[i][i] = true;
for (int j = i-1;j>=0;j--){
if (S.charAt(i)==S.charAt(j)){
if (i-j==1){
dp[j][i] = true;
}else {
dp[j][i] = dp[j+1][i-1];
}
}
}
}
int len = S.length();
int dp2[] = new int[len+1];
for (int i = k;i<=len;i++){
dp2[i] = dp2[i-1];
for (int j = i-k+1;j>0;j--){
if (dp[j-1][i-1]){
dp2[i] = Math.max(dp2[i],dp2[j-1]+1);
}
}
}
return dp2[len];
}
}
|
