手撕准备

无重复字符的最长子串

给定一个字符串 s ，请你找出其中不含有重复字符的 最长子串 的长度。

示例 1:

输入: s = "abcabcbb"
输出: 3 
解释: 因为无重复字符的最长子串是 "abc"，所以其长度为 3。

示例 2:

输入: s = "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b"，所以其长度为 1。

分析：双指针，l是左边，i是右边，不断变换l，如果遇到相同的元素，则改变l，l变为最后出现相同值得下一个位置。max是存储最大长度。

代码为：

class Solution {
    public int lengthOfLongestSubstring(String s) {
        Map<Character,Integer> map = new HashMap<>();
        int l = 0;
        int max =0;
        for (int i = 0;i<s.length();i++){
            char ch = s.charAt(i);
            if (map.containsKey(ch)){
                l = Math.max(l,map.get(ch));
            }
            max = Math.max(max,i-l+1);
            map.put(ch,i+1);
        }
        return max;
    }
}

LRU

class LRUCache {
    class TwoLinked{
        int value;
        int key;
        TwoLinked pre;
        TwoLinked next;
        public TwoLinked(){}
        public TwoLinked(int key,int value){
            this.key = key;
            this.value = value;
        }
    }

    Map<Integer,TwoLinked> map = new HashMap<>();
    int size;
    int capacity;
    TwoLinked head;
    TwoLinked tail;
    public LRUCache(int capacity) {
        this.size = 0;
        this.capacity = capacity;
        head = new TwoLinked();
        tail = new TwoLinked();
        head.next = tail;
        tail.pre = head;
    }

    public int get(int key) {
        TwoLinked twoLinked = map.get(key);
        if (twoLinked!=null){
            int v = twoLinked.value;
            removeToHead(twoLinked);
            return v;
        }else {
            return -1;
        }
    }

    public void put(int key, int value) {
        TwoLinked twoLinked1 = map.get(key);

        if (twoLinked1!=null){
            twoLinked1.value  =value;
            removeToHead(twoLinked1);
        }else {
            if (map.size()==capacity){
                map.remove(tail.pre.key);
                deleteLastLinked();
                size--;
            }
            TwoLinked newLinked = new TwoLinked(key, value);
            map.put(key,newLinked);
            addHeadLinked(newLinked);
            ++size;
        }
    }
    public void deleteLastLinked(){
        deleteLinked(tail.pre);
    }
    public void removeToHead(TwoLinked linked){
        deleteLinked(linked);
        addHeadLinked(linked);
    }
    public void deleteLinked(TwoLinked linked){
        linked.next.pre = linked.pre;
        linked.pre.next = linked.next;
    }
    public void addHeadLinked(TwoLinked linked){
        linked.next = head.next;
        linked.pre = head;
        head.next.pre = linked;

        head.next = linked;
    }

}

/**
 * Your LRUCache object will be instantiated and called as such:
 * LRUCache obj = new LRUCache(capacity);
 * int param_1 = obj.get(key);
 * obj.put(key,value);
 */

K个一组翻转链表

给你链表的头节点 head ，每 k 个节点一组进行翻转，请你返回修改后的链表。

k 是一个正整数，它的值小于或等于链表的长度。如果节点总数不是 k 的整数倍，那么请将最后剩余的节点保持原有顺序。

你不能只是单纯的改变节点内部的值，而是需要实际进行节点交换。

示例 1：

输入：head = [1,2,3,4,5], k = 2
输出：[2,1,4,3,5]

代码为：

class Solution {
    public ListNode reverseKGroup(ListNode head, int k) {
        ListNode dummy = new ListNode(0);
        dummy.next = head;
        ListNode pre = dummy;
        ListNode end = dummy;
        while (end!=null){
            for (int i = 0;i<k && end!=null;i++){
                end = end.next;
            }
            if (end==null) break;
            ListNode start = pre.next;
            ListNode next = end.next;
            end.next = null;
            pre.next = reverse(start);
            start.next = next;
            pre = start;
            end = pre;
        }
        return dummy.next;
    }
    public ListNode reverse(ListNode start){
        ListNode pre = null;
        ListNode cur = start;
        while (cur!=null){
            ListNode next = cur.next;
            cur.next = pre;
            pre = cur;
            cur = next;
        }
        return pre;
    }
}

数组中的第K个最大元素

给定整数数组 nums 和整数 k，请返回数组中第 k 个最大的元素。请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。

示例 1:

输入: [3,2,1,5,6,4], k = 2
输出: 5

优化快速排序和堆排序

快速代码为：

class Solution {
    public static int findKthLargest(int[] nums, int k) {
        int res = sort(nums,0,nums.length-1,nums.length-k);
        return res;
    }
    public static int sort(int nums[],int l,int r,int k){
        if(l<=r){
            int index = quickSort(nums,l,r);
            //优化
            if (index==k) return nums[k];
            else return index<k ? sort(nums,index+1,r,k):sort(nums,l,index-1,k);
        }
        return 0;
    }
    public static int quickSort(int nums[],int l,int r){
        int t = nums[l];
        while (l<r){
            while (l<r && nums[r]>=t){
                r--;
            }
            if (nums[r]<t){
                nums[l] = nums[r];
            }
            while (l<r && nums[l]<=t){
                l++;
            }
            if (nums[l]>t){
                nums[r] = nums[l];
            }
        }
        nums[l] = t;
        return l;
    }
}

堆排序代码为：

class Solution {
    public static int findKthLargest(int[] nums, int k) {
        int i = HeapSort(nums, k);
        return i;
    }
    public static int HeapSort(int nums[],int k){
        for (int i = nums.length/2-1;i>=0;i--){
            sort(nums,i,nums.length);
        }
        //优化
        for (int i = nums.length-1;i>=nums.length-k;i--){
            if (nums[i]<nums[0]){
                int t = nums[i];
                nums[i] = nums[0];
                nums[0] =t;
            }
            sort(nums,0,i);
        }
        return nums[nums.length-k];
    }
    public static void sort(int nums[],int i,int n){
        int t = nums[i];
        for (int a = 2*i+1;a<n;a = 2*a+1){
            if (a+1<n && nums[a]<nums[a+1]){
                a++;
            }
            if (nums[i]<nums[a]){
                nums[i] = nums[a];
                i = a;
            }else break;
            nums[a] = t;
        }
    }
}

二叉树锯齿形层序遍历

给你二叉树的根节点 root ，返回其节点值的 锯齿形层序遍历 。（即先从左往右，再从右往左进行下一层遍历，以此类推，层与层之间交替进行）。

示例 1：

输入：root = [3,9,20,null,null,15,7]
输出：[[3],[20,9],[15,7]]

示例 2：

输入：root = [1]
输出：[[1]]

示例 3：

输入：root = []
输出：[]

分析：使用一个数来控制奇偶，根节点为设置为第一层，所以奇数正序，偶数逆序。

代码为：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public static List<List<Integer>> zigzagLevelOrder(TreeNode root) {
        List<List<Integer>> res = new ArrayList<>();
        if (root == null) return res;
        int count = 1;

        Deque<TreeNode> queue = new LinkedList<>();
        queue.addLast(root);
        while (!queue.isEmpty()) {
            int size = queue.size();
            Deque<Integer> list1 = new LinkedList<>();
            while (size-- > 0) {
                TreeNode node = queue.poll();
                if (count % 2 == 1) {
                    //如果该层是奇数，则正序存放
                    list1.addLast(node.val);
                } else {
                    //如果该层是偶数，则逆序存放
                    list1.addFirst(node.val);
                }
                if (node.left != null) {
                    queue.add(node.left);
                }
                if (node.right != null) {
                    queue.add(node.right);
                }
            }
            res.add(new ArrayList<>(list1));
            count++;
        }
        return res;
    }
}

三数之和

给你一个整数数组 nums ，判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ，同时还满足 nums[i] + nums[j] + nums[k] == 0 。请

你返回所有和为 0 且不重复的三元组。

注意：答案中不可以包含重复的三元组。

示例1：

输入：nums = [-1,0,1,2,-1,-4]
输出：[[-1,-1,2],[-1,0,1]]
解释：
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。
不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。
注意，输出的顺序和三元组的顺序并不重要。

示例 2：

输入：nums = [0,1,1]
输出：[]
解释：唯一可能的三元组和不为 0 。

示例 3：

输入：nums = [0,0,0]
输出：[[0,0,0]]
解释：唯一可能的三元组和为 0 。

分析：

固定一个数i，改变l和r。

代码为：

class Solution {
    public List<List<Integer>> threeSum(int[] nums) {
        int n = nums.length;
        Arrays.sort(nums);
        List<List<Integer>> res = new ArrayList<>();
        for (int i = 0;i<n;i++){
            if (nums[i]>0) continue;
            if (i-1>=0 && nums[i]==nums[i-1]) continue;
            int l = i+1;
            int r = n-1;
            while (l<r){
                int sum = nums[i]+nums[l]+nums[r];
                if (sum==0){
                    res.add(Arrays.asList(nums[i],nums[l],nums[r]));
                    while (l+1<n && nums[l+1]==nums[l]) l++;
                    while (r-1>=0 && nums[r]==nums[r-1]) r--;
                    l++;
                    r--;
                }else if (sum<0){
                    l++;
                }else {
                    r--;
                }
            }
        }
        return res;
    }
}

搜索旋转排序数组

整数数组 nums 按升序排列，数组中的值 互不相同 。

在传递给函数之前，nums 在预先未知的某个下标 k（0 <= k < nums.length）上进行了 旋转，使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]（下标 从 0 开始 计数）。例如， [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。

给你 旋转后 的数组 nums 和一个整数 target ，如果 nums 中存在这个目标值 target ，则返回它的下标，否则返回 -1 。

你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。

示例 1：

输入：nums = [4,5,6,7,0,1,2], target = 0
输出：4

示例 2：

输入：nums = [4,5,6,7,0,1,2], target = 3
输出：-1

分析：二分法，首先将数组进行二分，二分之后两边肯定有一个有序有一个无序，在有序的一边进行查找。无序的一边再进行一分为二。

代码为：

class Solution {
    public int search(int[] nums, int target) {
            int n = nums.length;
            if (n==0) return -1;
            if (n==1) return nums[0]==target?0:-1;
            int left = 0;
            int right = n-1;
            while (left<right){
                int mid = (left+right)/2;
                if (target==nums[mid]) return mid;
                //如果左边有序
                if (nums[0]<=nums[mid]){
                    //看目标值是否在左边
                    if (target<nums[mid] && target>=nums[0]){
                        right = mid-1;
                    }else left = mid + 1;
                //如果右边有序
                }else {
                    //看目标值是否在右边
                    if (target>nums[mid] && target<=nums[n-1]){
                        left = mid + 1;
                    }else right = mid - 1;
                }
            }
            if (nums[left]==target) return left;
            return -1;
        }
}

接雨水

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例 1：

输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。

分析：每个可以接受雨水的位置是，左右两边最大高度的最小值-该位置的高度。

因此我们可以定义两个数组，来存储每个位置 左边的最大高度 和 右边的最大高度

leftMax[i] = Math.max(leftMax[i-1],height[i]);

rightMax[i] = Math.max(rightMax[i+1],height[i]);

代码为：

class Solution {
    public int trap(int[] height) {
        int n = height.length;
        int leftMax[] = new int[n];
        int rightMax[] = new int[n];
        leftMax[0] = height[0];
        for (int i = 1;i<n;i++){
            leftMax[i] = Math.max(leftMax[i-1],height[i]);
        }
        rightMax[n-1] = height[n-1];
        for (int i = n-2;i>=0;i--){
            rightMax[i] = Math.max(rightMax[i+1],height[i]);
        }
        int res = 0;
        for (int i = 0;i<n;i++){
            res+=Math.min(rightMax[i],leftMax[i])-height[i];
        }
        return res;
    }
}

分析：使用双指针，来表示左右连边的最大高度。

代码为:

class Solution {
    public int trap(int[] height) {
        int n = height.length;
        int leftMax = 0;
        int rightMax = 0;
        int left = 0;
        int right = n-1;
        int res = 0;
        for (int i = 0;i<n;i++){
            leftMax = Math.max(leftMax,height[left]);
            rightMax = Math.max(rightMax,height[right]);
            if (height[left]<height[right]){
                res+=leftMax-height[left];
                ++left;
            }else {
                res+=rightMax-height[right];
                --right;
            }
        }
        return res;
    }
}

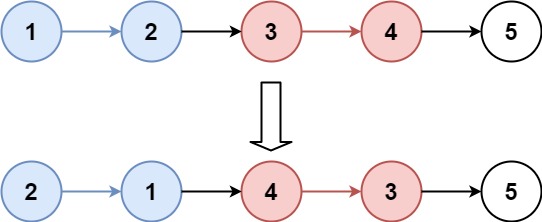
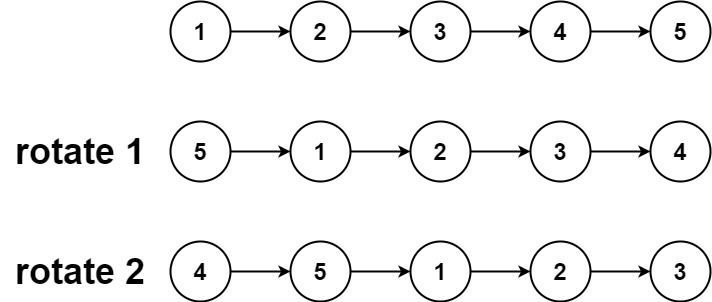
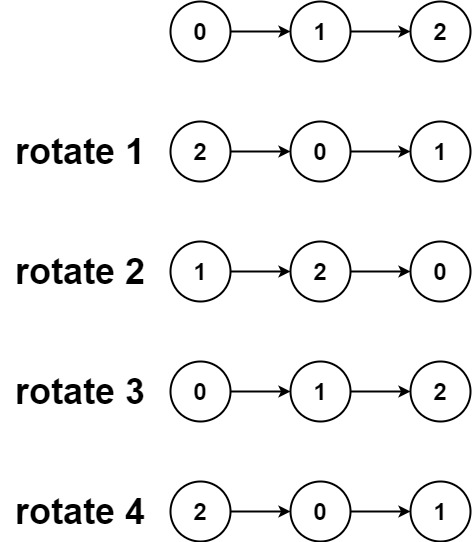
旋转链表

给你一个链表的头节点 head ，旋转链表，将链表每个节点向右移动 k 个位置。

示例 1：

输入：head = [1,2,3,4,5], k = 2
输出：[4,5,1,2,3]

示例 2：

输入：head = [0,1,2], k = 4
输出：[2,0,1]

分析：就是将，从尾部开始的第k个节点作为头结点，原来的头结点作为链表结尾的下一个节点。

我们仅需要向右移动 k mod n 次即可。因为每 n 次移动都会让链表变为原状。

• 我们首先计算出链表的长度 n，
• 并找到该链表的末尾节点，将其与头节点相连。这样就得到了闭合为环的链表。
• 然后我们找新链表的最后一个节点，进行断开。

代码为：

class Solution {
    public ListNode rotateRight(ListNode head, int k) {
        if (head==null || head.next==null||k==0) return head;
        ListNode p = head;
        int n = 1;
        //求出链表的长度
        while (p.next!=null){
            p = p.next;
            n++;
        }
        //在哪断开
        int a = n-k%n;
        if (a==n){
            return head;
        }
         //将链表弄成环形链表
        p.next = head;
        //找到断开点
        while (a-->0){
            p = p.next;
        }
        ////结果链表的头部为断开点的下一个节点
        ListNode res = p.next;
        //断开点的下一个节点置为null
        p.next = null;
        return res;
    }
}

买股票的最佳时期

给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。

你只能选择 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。

返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。

示例 1：

输入：[7,1,5,3,6,4]
输出：5
解释：在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
     注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格；同时，你不能在买入前卖出股票。

示例 2：

输入：prices = [7,6,4,3,1]
输出：0
解释：在这种情况下, 没有交易完成, 所以最大利润为 0。

分析：如果我是在历史最低点买的股票就好了！太好了，在题目中，我们只要用一个变量记录一个历史最低价格 minprice，我们就可以假设自己的股票是在那天买的。那么我们在第 i 天卖出股票能得到的利润就是 prices[i] - minprice。

代码为：

class Solution {
    public int maxProfit(int[] prices) {
        int minPrice = Integer.MAX_VALUE;
        int max = 0;
        for (int i = 0;i<prices.length;i++){
            if (prices[i]<minPrice){
                minPrice = prices[i];
            }
            if (prices[i]-minPrice>max){
                max = prices[i]-minPrice;
            }
        }
        return max;
    }
}

合并K个升序链表

给你一个链表数组，每个链表都已经按升序排列。

请你将所有链表合并到一个升序链表中，返回合并后的链表。

示例 1：

输入：lists = [[1,4,5],[1,3,4],[2,6]]
输出：[1,1,2,3,4,4,5,6]
解释：链表数组如下：
[
  1->4->5,
  1->3->4,
  2->6
]
将它们合并到一个有序链表中得到。
1->1->2->3->4->4->5->6

示例 2：

输入：lists = []
输出：[]

示例 3：

输入：lists = [[]]
输出：[]

分析：将链表两两合并。像合并两个有序链表一样

代码为：

class Solution {
    public ListNode mergeKLists(ListNode[] lists) {
        ListNode res = null;
        for (int i = 0;i< lists.length;i++){
            res = merge(res,lists[i]);
        }
        return res;
    }
    public ListNode merge(ListNode a,ListNode b){
        ListNode pre = new ListNode(0);
        ListNode p = pre;
        ListNode aa = a;
        ListNode bb = b;
        while (aa!=null && bb!=null){
            if (aa.val<bb.val){
                p.next = aa;
                aa = aa.next;
            }else {
                p.next = bb;
                bb = bb.next;
            }
            p = p.next;
        }
        p.next=aa==null?bb:aa;
        return pre.next;
    }
}

螺旋数组

private static List<Integer> spiralOrder(int[][] matrix) {
        LinkedList<Integer> result = new LinkedList<>();
        if(matrix==null||matrix.length==0) return result;
        int left = 0;
        int right = matrix[0].length - 1;
        int top = 0;
        int bottom = matrix.length - 1;
        int numEle = matrix.length * matrix[0].length;
        while (numEle >= 1) {
            for (int i = left; i <= right && numEle >= 1; i++) {
                result.add(matrix[top][i]);
                numEle--;
            }
            top++;
            for (int i = top; i <= bottom && numEle >= 1; i++) {
                result.add(matrix[i][right]);
                numEle--;
            }
            right--;
            for (int i = right; i >= left && numEle >= 1; i--) {
                result.add(matrix[bottom][i]);
                numEle--;
            }
            bottom--;
            for (int i = bottom; i >= top && numEle >= 1; i--) {
                result.add(matrix[i][left]);
                numEle--;
            }
            left++;
        }
        return result;
    }

最有效括号

class Solution {
    public int longestValidParentheses(String s) {
        int maxans = 0;
        Deque<Integer> stack = new LinkedList<Integer>();
        stack.push(-1);
        for (int i = 0; i < s.length(); i++) {
            if (s.charAt(i) == '(') {
                stack.push(i);
            } else {
                stack.pop();
                if (stack.isEmpty()) {
                    stack.push(i);
                } else {
                    maxans = Math.max(maxans, i - stack.peek());
                }
            }
        }
        return maxans;
    }
}

最长递增子序列

class Solution {
    public int lengthOfLIS(int[] nums) {
        if (nums.length == 0) {
            return 0;
        }
        int[] dp = new int[nums.length];
        dp[0] = 1;
        int maxans = 1;
        for (int i = 1; i < nums.length; i++) {
            dp[i] = 1;
            for (int j = 0; j < i; j++) {
                if (nums[i] > nums[j]) {
                    dp[i] = Math.max(dp[i], dp[j] + 1);
                }
            }
            maxans = Math.max(maxans, dp[i]);
        }
        return maxans;
    }
}

二叉树的最近公共祖先

class Solution {
    Map<Integer, TreeNode> parent = new HashMap<Integer, TreeNode>();
    Set<Integer> visited = new HashSet<Integer>();

    public void dfs(TreeNode root) {
        if (root.left != null) {
            parent.put(root.left.val, root);
            dfs(root.left);
        }
        if (root.right != null) {
            parent.put(root.right.val, root);
            dfs(root.right);
        }
    }

    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        dfs(root);
        while (p != null) {
            visited.add(p.val);
            p = parent.get(p.val);
        }
        while (q != null) {
            if (visited.contains(q.val)) {
                return q;
            }
            q = parent.get(q.val);
        }
        return null;
    }
}

括号生成

class Solution {
    public List<String> generateParenthesis(int n) {
        List<String> ans = new ArrayList<String>();
        backtrack(ans, new StringBuilder(), 0, 0, n);
        return ans;
    }

    public void backtrack(List<String> ans, StringBuilder cur, int open, int close, int max) {
        if (cur.length() == max * 2) {
            ans.add(cur.toString());
            return;
        }
        if (open < max) {
            cur.append('(');
            backtrack(ans, cur, open + 1, close, max);
            cur.deleteCharAt(cur.length() - 1);
        }
        if (close < open) {
            cur.append(')');
            backtrack(ans, cur, open, close + 1, max);
            cur.deleteCharAt(cur.length() - 1);
        }
    }
}

最短无序连续子数组

class Solution {
    public int findUnsortedSubarray(int[] nums) {
        int n = nums.length;
        int maxn = Integer.MIN_VALUE, right = -1;
        int minn = Integer.MAX_VALUE, left = -1;
        for (int i = 0; i < n; i++) {
            if (maxn > nums[i]) {
                right = i;
            } else {
                maxn = nums[i];
            }
            if (minn < nums[n - i - 1]) {
                left = n - i - 1;
            } else {
                minn = nums[n - i - 1];
            }
        }
        return right == -1 ? 0 : right - left + 1;
    }
}

class Solution {
    public int findUnsortedSubarray(int[] nums) {
        //初始化
        int len = nums.length;
        int min = nums[len-1];
        int max = nums[0];
        int begin = 0, end = -1;
        //遍历
        for(int i = 0; i < len; i++){
            if(nums[i] < max){      //从左到右维持最大值，寻找右边界end
                end = i;
            }else{
                max = nums[i];
            }
            
            if(nums[len-i-1] > min){    //从右到左维持最小值，寻找左边界begin
                begin = len-i-1;
            }else{
                min = nums[len-i-1];
            }            
        }
        return end-begin+1;
    }
}