岛屿问题

岛屿问题

我们所熟悉的 DFS（深度优先搜索）问题通常是在树或者图结构上进行的。

只需要在树的遍历的基础上进行改进就好。

树是访问相邻的左右子树节点，而图是访问上下左右的节点。

树是要判断该root节点是否为null，而图是要判断该节点是否出界。

树的框架代码：

1
2
3
4
5
6
7
8
9
void traverse(TreeNode root) {
    // 判断 base case
    if (root == null) {
        return;
    }
    // 访问两个相邻结点：左子结点、右子结点
    traverse(root.left);
    traverse(root.right);
}

网络的框架代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
boolean used[][] = new int[grid.length][grid[0].length];
void dfs(int[][] grid, int r, int c) {
    // 判断 base case，判断坐标是否在网格中
    if (i<0 || j<0 || i>grid.length-1 || j>grid[0].length-1 || used[i][j] || grid[i][j]=='0') return;
    
    grid[r][c] = true; // 将格子标记为「已遍历过」
    
    // 访问上、下、左、右四个相邻结点
    dfs(grid, r - 1, c);
    dfs(grid, r + 1, c);
    dfs(grid, r, c - 1);
    dfs(grid, r, c + 1);
}

岛屿数量-leetCode200

给你一个由 '1'（陆地）和 '0'（水）组成的的二维网格，请你计算网格中岛屿的数量。

岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。

此外，你可以假设该网格的四条边均被水包围。

示例 1：

1
2
3
4
5
6
7
输入：grid = [
  ["1","1","1","1","0"],
  ["1","1","0","1","0"],
  ["1","1","0","0","0"],
  ["0","0","0","0","0"]
]
输出：1

示例 2：

1
2
3
4
5
6
7
输入：grid = [
  ["1","1","0","0","0"],
  ["1","1","0","0","0"],
  ["0","0","1","0","0"],
  ["0","0","0","1","1"]
]
输出：3

深度

首先遍历数组，如果数组的元素为1，则遍历它的上下左右。而它的上下左右元素也使用同样的方法进行上下左右的遍历。

代码为：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    boolean used[][];
    int count = 0;
    public int numIslands(char[][] grid) {
        used = new boolean[grid.length][grid[0].length];
        for (int i =0;i<grid.length;i++){
            for (int j = 0;j<grid[0].length;j++){
                if (grid[i][j]=='1' && !used[i][j]){
                    dfs(grid,i,j,used);
                    count++;
                }
            }
        }
        return count;
    }
    public void dfs(char[][] grid,int i,int j,boolean used[][]){
        if (i<0 || j<0 || i>grid.length-1 || j>grid[0].length-1 || used[i][j] || grid[i][j]=='0') return;
        used[i][j] = true;
        dfs(grid,i+1,j,used);
        dfs(grid,i-1,j,used);
        dfs(grid,i,j+1,used);
        dfs(grid,i,j-1,used);
    }
}

广度

遍历网路，将为1的格子加入到队列中，开始进行广度优先搜索。在广度优先搜索的过程中，每个搜索到的 11 都会被重新标记为 00。直到队列为空，搜索结束。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
class Solution {
    public int numIslands(char[][] grid) {
        boolean used[][] = new boolean[grid.length][grid[0].length];
        Queue<Integer> queue = new LinkedList<>();
        int count = 0;
        for (int i = 0;i<grid.length;i++){
            for (int j = 0;j<grid[0].length;j++){
                //如果为1且没有访问过，则加入到队列中，加入队列时使用i * grid[0].length + j，方便通过值算出横纵坐标
                    if (grid[i][j]=='1' && !used[i][j]) {
                        count++;
                        queue.add(i * grid[0].length + j);
                        while (!queue.isEmpty()) {
                            int a = queue.remove();
                            int row = a / grid[0].length;
                            int col = a % grid[0].length;
                            if (row-1>=0 && grid[row-1][col]=='1' && !used[row-1][col]){
                                queue.add((row-1)*grid[0].length+col);
                                used[row-1][col] = true;
                            }
                            if (row+1<grid.length && grid[row+1][col]=='1' && !used[row+1][col]){
                                queue.add((row+1)*grid[0].length+col);
                                used[row+1][col] = true;
                            }
                            if (col-1>=0 && grid[row][col-1]=='1' && !used[row][col-1]){
                                queue.add((row)*grid[0].length+col-1);
                                used[row][col-1] = true;
                            }
                            if (col+1<grid[0].length && grid[row][col+1]=='1' && !used[row][col+1]){
                                queue.add((row)*grid[0].length+col+1);
                                used[row][col+1] = true;
                            }
                        }
                    }
            }
        }
        return count;
    }
}

岛屿的周长

递归

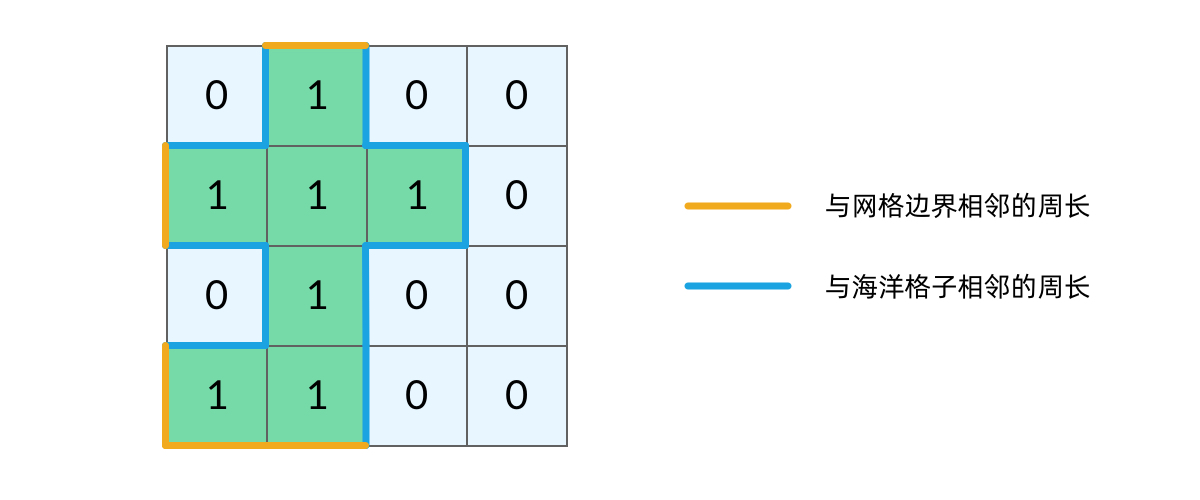
将岛屿周长中的边分为两类

代码为：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
    int count = 0;
    public int islandPerimeter(int[][] grid) {
        boolean used[][] = new boolean[grid.length][grid[0].length];
        int res = 0;
        for (int i = 0;i<grid.length;i++){
            for (int j = 0;j<grid[0].length;j++){
                if (grid[i][j]==1 && !used[i][j]){
                    //由于所有的陆地都是相连的，所以一次就行
                    return dfs(grid,i,j,used);
                }
            }
        }
        return 0;
    }
    public int dfs(int grid[][],int i,int j,boolean used[][]){
        //当是黄色边界以及，周围是海洋的蓝色边界时+1
        if (i<0 || j<0 || i>grid.length-1 || j>grid[0].length-1 || grid[i][j]==0) {
            return 1;
        }
        //当前格子是已经遍历过的陆地格子
        if(used[i][j]) return 0;
        used[i][j] = true;
        return dfs(grid,i+1,j,used)
        + dfs(grid,i-1,j,used)
        + dfs(grid,i,j+1,used)
        + dfs(grid,i,j-1,used);
    }
}

迭代

我们可以遍历每个陆地格子，看其四个方向是否为边界或者水域，如果是，将这条边的贡献（即 1）加入答案 ans 中即可。

代码为：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
    static int[] dx = {0, 1, 0, -1};
    static int[] dy = {1, 0, -1, 0};

    public int islandPerimeter(int[][] grid) {
        int n = grid.length, m = grid[0].length;
        int ans = 0;
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < m; ++j) {
                if (grid[i][j] == 1) {
                    int cnt = 0;
                    for (int k = 0; k < 4; ++k) {
                        int tx = i + dx[k];
                        int ty = j + dy[k];
                        if (tx < 0 || tx >= n || ty < 0 || ty >= m || grid[tx][ty] == 0) {
                            cnt += 1;
                        }
                    }
                    ans += cnt;
                }
            }
        }
        return ans;
    }
}

方法三

或者设置遍历每个为 1 的方格，初始周长都为4，遍历该方格的上下左右，如果为1，则减1。

代码为：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
    public int islandPerimeter(int[][] grid) {
        int sum = 0;
        for (int i =0;i<grid.length;i++){
            for (int j = 0;j<grid[i].length;j++){
                if (grid[i][j]==1){
                    sum+=dfs(grid,i,j);
                }
            }
        }
        return sum;
    }
    public int dfs(int [][]grid,int i,int j){
        int a = 4;
        if (i>=1 && grid[i-1][j]==1){
            a--;
        }
        if (i+1<grid.length && grid[i+1][j]==1){
            a--;
        }
        if (j>=1 && grid[i][j-1]==1){
            a--;
        }
        if (j+1<grid[i].length && grid[i][j+1]==1){
            a--;
        }
        return a;
    }
}

岛屿的最大面积

给你一个大小为 m x n 的二进制矩阵 grid 。

岛屿 是由一些相邻的 1 (代表土地) 构成的组合，这里的「相邻」要求两个 1 必须在 水平或者竖直的四个方向上 相邻。你可以假设 grid 的四个边缘都被 0（代表水）包围着。

岛屿的面积是岛上值为 1 的单元格的数目。

计算并返回 grid 中最大的岛屿面积。如果没有岛屿，则返回面积为 0 。

示例 1：

img

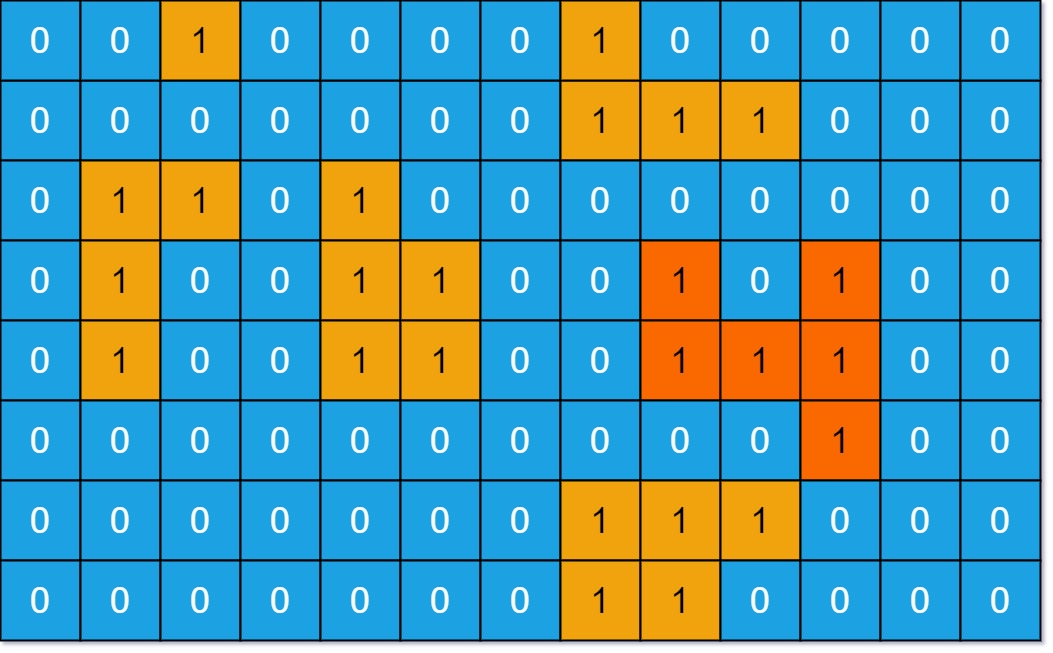
1
2
3
输入：grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]
输出：6
解释：答案不应该是 11 ，因为岛屿只能包含水平或垂直这四个方向上的 1 。

示例 2：

1
2
输入：grid = [[0,0,0,0,0,0,0,0]]
输出：0

递归

与岛屿的数量很相似，这个是求岛屿中的最大岛屿的数量。

代码为：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
    static int count;
    static int max;
    public static int maxAreaOfIsland(int[][] grid) {
        boolean used[][] = new boolean[grid.length][grid[0].length];
        int ans = 0;
        for (int i = 0;i<grid.length;i++){
            for (int j = 0;j<grid[0].length;j++){
                if (grid[i][j]==1){
                    count = 0;
                    max = 0;
                    ans = Math.max(dfs(grid,i,j,used),ans);
                }
            }
        }
        return ans;
    }
    public static int dfs(int grid[][],int i,int j,boolean used[][]){
        if (i<0 || j<0 || i>used.length-1 || j>grid[0].length-1 || grid[i][j]==0 || used[i][j]){
            return 0;
        }
        if (grid[i][j]==1){
            count++;
            max = Math.max(max,count);
        }

        used[i][j] = true;
        dfs(grid,i-1,j,used);
        dfs(grid,i+1,j,used);
        dfs(grid,i,j-1,used);
        dfs(grid,i,j+1,used);
        return max;
    }
}

迭代

遍历网络，如果网格是1，则加入到队列中，从队列中取数，遍历岛屿的数量，维护一个max，求岛屿中数量大最大值。

下面这段代码使用一个栈存储数据，该数据是i*grid[0].length+j，因为再取出数据后，可以通过这个数得到横纵坐标。

也可以使用两个栈去分别存储，横纵坐标。

代码为：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
    static int dx[] = new int[]{0,0,1,-1};
    static int dy[] = new int[]{1,-1,0,0};
    public static int maxAreaOfIsland(int[][] grid) {
        boolean used[][] = new boolean[grid.length][grid[0].length];
        Queue<Integer> queue = new LinkedList<>();
        int max = 0;
        for (int i =0;i<grid.length;i++){
            for (int j = 0;j<grid[0].length;j++){
                if (grid[i][j]==1){
                    queue.add(i*grid[0].length+j);
                    used[i][j] = true;
                    int count = 1;
                    while (!queue.isEmpty()){
                        int a = queue.remove();
                        int row = a/grid[0].length;
                        int col = a%grid[0].length;
                        for (int f = 0;f<4;f++){
                            int newx = row+dx[f];
                            int newy = col+dy[f];
                            if (newx>=0 && newy>=0 && newx<grid.length && newy<grid[0].length && grid[newx][newy]==1 && !used[newx][newy]){
                                count++;
                                queue.add(newx*grid[0].length+newy);
                                used[newx][newy] = true;
                            }
                        }
                    }
                    max = Math.max(max,count);
                }
            }
        }
        return max;
    }
}
算法 > 岛屿问题
岛屿问题
http://example.com/2022/11/04/岛屿问题/
作者
zlw
发布于
2022年11月4日
许可协议