得物笔试

算法一（前序+中序输出后序）

根据树的前序和中序输出后序

分析：

首先前序遍历的第一个节点一定为根节点，

找到中序遍历中的根节点，则根节点两边的数字就是左右子树。

例如：前序：1 2 4 5 3 6 7 ，中序：4 2 5 1 6 3 7，则根节点为1，根节点的左子树：4 2 5 ，根节点的右子树为：6 3 7.

找到左右子树后，分别对左右子树进行同样的操作。因此递归可以实现。

通过遍历前序遍历的节点，找到中序遍历中出现的位置，则左右两边就是左右子树

代码为：

import java.util.*;

public class Main {
    public static void main(String[] args) {
//        Scanner input = new Scanner(System.in);
//        int N = input.nextInt();
//        int[] preorder = new int[N];
//        int[] inorder = new int[N];
//        for (int i = 0; i < N; i++) {
//            preorder[i] = input.nextInt();
//        }
//        for (int i = 0; i < N; i++) {
//            inorder[i] = input.nextInt();
//        }
        int preorder[] = new int[]{1,2,4,5,3,6,7};
        int inorder[] = new int[]{4,2,5,1,6,3,7};
        new Main().buildTree(preorder, inorder);
    }
    //存储前序遍历的节点在中序遍历中的位置
    Map<Integer, Integer> map = new HashMap<>();
    int[] preorder;
    public void buildTree(int[] preorder, int[] inorder) {
        this.preorder = preorder;
        for (int i = 0; i < inorder.length; i++) {
            map.put(inorder[i], i);
        }
        build(0, preorder.length-1, 0, inorder.length-1);
    }
    private void build(int preStart, int preEnd, int inStart, int inEnd) {
        if (preStart > preEnd || inStart > inEnd) {
            return ;
        }
        //前序遍历的节点值
        int rootVal = preorder[preStart];
        //获取该节点在中序遍历中的下标
        int rootIndex = map.get(rootVal);
        //计算左子树的数量，
        int leftNum = rootIndex - inStart;//当遍历右子树的左子树时有用。
        //递归遍历
        build(preStart+1, preStart+leftNum, inStart, rootIndex-1);
        build(preStart+leftNum+1, preEnd, rootIndex+1, inEnd);
        System.out.print(rootVal + " ");
    }
}

后序+中序输出前序

代码：

import java.util.*;

public class Main {
    static int inorder[] = new int[]{3, 2, 4, 1, 6, 5};
    static int lastorder[] = new int[]{3, 4, 2, 6, 5, 1};
    static Map<Integer,Integer> map = new HashMap<>();
    public static void main(String[] args) {
        for (int i = 0;i<inorder.length;i++){
            map.put(inorder[i],i);
        }
        int n = inorder.length;
        dfs(0,n-1,0,n-1);
    }
    public static void dfs(int inl,int inr,int lal,int lar){
        if (lal>lar) return;
        int t = map.get(lastorder[lar]);
        int leftNum = t-inl-1;//因为后序遍历的左子树部分，没有根节点，根节点在最后，所以要-1.
        System.out.print(lastorder[lar]+ " ");
        dfs(inl,t-1,lal,lal+leftNum);
        dfs(t+1,inr,lal+leftNum+1,lar-1);

    }
}

算法二（双栈排序）

给定一个乱序的栈，设计算法将其升序排列。

ps: 允许额外使用一个栈来辅助操作

分析：

通过一个辅助栈来给栈排序

也就是保持辅助栈中的元素是单调递增的。

如果遍历原栈的栈顶元素小于辅助栈的栈顶元素，则将辅助栈的元素出栈，加入到原栈中的尾部。

再将目前遍历到的元素加入到辅助栈的栈顶。始终保持辅助栈是单调的。

依次遍历，知道原栈所有的元素已经加入到辅助栈中排序完成。

代码：

import java.util.*;

public class Main3 {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n  = scanner.nextInt();
        Deque<Integer> stack = new ArrayDeque<>();
        for (int i = 0;i<n;i++){
            stack.addLast(scanner.nextInt());
        }
        Deque<Integer> stack2 = new ArrayDeque<>();
        if (stack.isEmpty()) {
            System.out.println(stack.toString());
            return;
        }
        while (!stack.isEmpty()){
            int t = stack.pollLast();
            while (!stack2.isEmpty() && stack2.peekLast()>t){
                stack.addLast(stack2.pollLast());
            }
            stack2.addLast(t);
        }
        System.out.println(stack2.toString());
    }
}

算法三（最小操作数）

给定一个原串和目标串，能对源串进行如下操作：
1.在给定位置插入一个字符
2.替换任意字符
3.删除任意字符 要求完成一下函数，返回最少的操作数，使得源串进行这些操作后等于目标串。源串和目标串长度都小于2000。

分析：

使用动态规划方法：

设置一个二维的dp数组，dp[i][j]表示原字符串前i个位置到目标字符串前j个位置所需要的最小操作数。

可以分为以下情况：

当原串和目标串都为空时：返回0

当原串为空，目标串不为空时，返回目标串的长度

当目标串为空，原串不为空时，返回原串的长度

如果都不为空：

​ 如果 i 和 j 的位置相等，则Math.min(dp[i-1][j-1],dp[i-1][j]+1,dp[i][j-1]+1),否则Math.min(dp[i-1][j-1]+1,dp[i-1][j]+1,dp[i][j-1]+1)

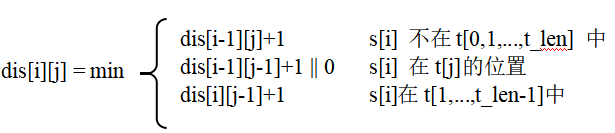
代码：

public class Main2 {
    public int minOperationCount(String source, String target) {
        int m = source.length();
        int n = target.length();
        if (m==0) return n;
        if (n==0) return m;
        int dp[][] = new int[m+1][n+1];
        dp[0][0] = 0;
        for (int i = 0;i<=m;i++){
            dp[i][0] = i;
        }
        for (int i = 0;i<=n;i++){
            dp[0][i] = i;
        }
        int f = 0;
        for (int i = 1;i<=m;i++){
            char ch = source.charAt(i);
            for (int j = 1;j<=n;j++){
                char ch2 = source.charAt(j);
                if (ch==ch2){
                  f = 0;
                }else f = 1;
                dp[i][j] = Math.min(dp[i-1][j-1]+f,Math.min(dp[i-1][j]+1,dp[i][j-1]+1));
            }
        }
        return dp[m][n];
    }
}