单词搜索
单词搜索
给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中,返回 true ;否则,返回 false 。
单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。
示例 1:
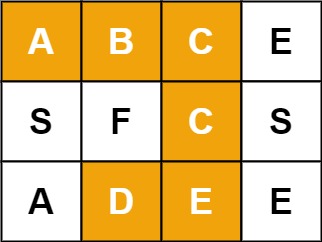
1 | |
示例 2:
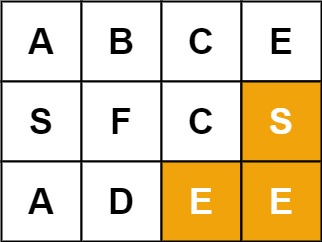
1 | |
示例 3:

1 | |
解法一
以
"SEE"为例,首先要选起点:遍历矩阵,找到起点S。起点可能不止一个,基于其中一个S,看看能否找出剩下的”EE”路径。
下一个字符E有四个可选点:当前点的上、下、左、右。
逐个尝试每一种选择。基于当前选择,为下一个字符选点,又有四种选择。
每到一个点做的事情是一样的。DFS 往下选点,构建路径。
当发现某个选择不对,不用继续选下去了,结束当前递归,考察别的选择。
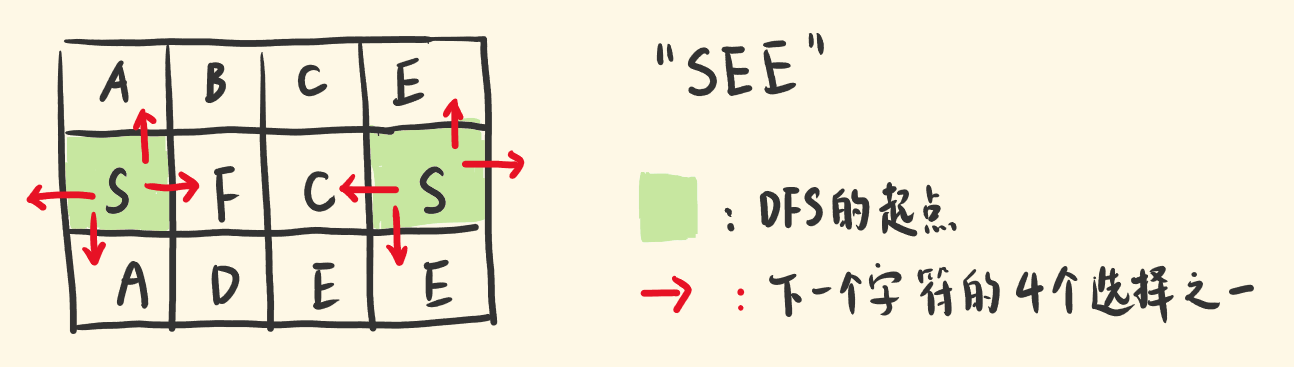
递归把握什么?
关注当前考察的点,处理它,其他丢给递归子调用去做。
- 判断当前选择的点,本身是不是一个错的点。
- 剩下的字符能否找到路径,交给递归子调用去做。
如果当前点是错的,不用往下递归了,返回false。否则继续递归四个方向,为剩下的字符选点。那么,哪些情况说明这是一个错的点:
当前的点,越出矩阵边界。
当前的点,之前访问过,不满足「同一个单元格内的字母不允许被重复使用」。
当前的点,不是目标点,比如你想找 E,却来到了 D。
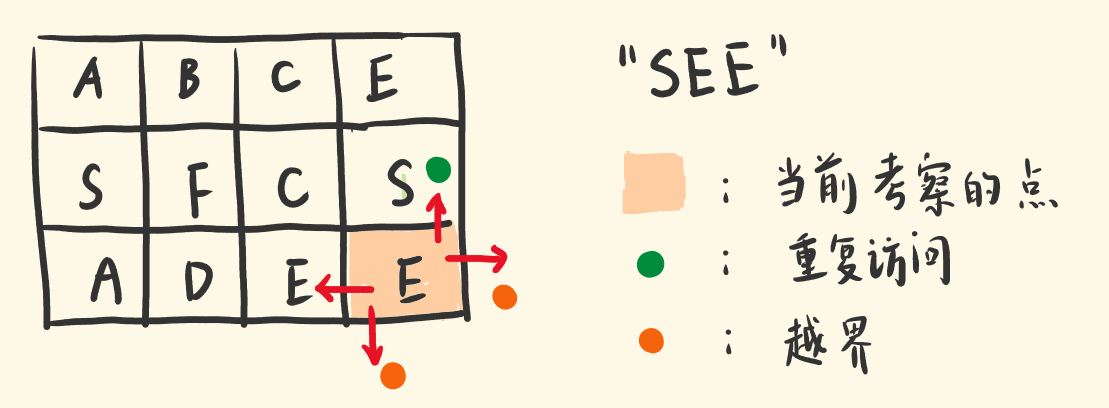
记录访问过的点
用一个二维矩阵 used,记录已经访问过的点,下次再选择访问这个点,就直接返回 false。
为什么要回溯?
有的选点是错的,选它就构建不出目标路径,不能继续选。要撤销这个选择,去尝试别的选择。
1 | |
如果第一个递归调用返回 false,就会执行||后的下一个递归调用
- 这里暗含回溯:当前处在[row,col],选择[row+1,col]继续递归,返回false的话,会撤销[row+1,col]这个选择,回到[row,col],继续选择[row-1,col]递归。
只要其中有一个递归调用返回 true,||后的递归就不会执行,即找到解就终止搜索,利用||的短路效应,把枝剪了。
如果求出 canFindRest 为 false,说明基于当前点不能找到剩下的路径,所以当前递归要返回false,还要在used矩阵中把当前点恢复为未访问,让它后续能正常被访问。
- 因为,基于当前路径,选当前点是不对的,但基于别的路径,走到这选它,有可能是对的。
什么时候返回 true?
在递归中,我们设置了所有返回 false 的情况。
当指针越界,此时已经考察完单词字符,意味着,在该递归分支中,为一个个字符选点,始终没有返回过 false,这些字符都选到对的点。所以指针越界就可以返回 true。
代码为:
1 | |
解法二
1 | |