三角形最小路径和

给定一个三角形 triangle ，找出自顶向下的最小路径和。

每一步只能移动到下一行中相邻的结点上。相邻的结点 在这里指的是 下标 与 上一层结点下标 相同或者等于 上一层结点下标 + 1 的两个结点。也就是说，如果正位于当前行的下标 i ，那么下一步可以移动到下一行的下标 i 或 i + 1 。

示例 1：

输入：triangle = [[2],[3,4],[6,5,7],[4,1,8,3]]
输出：11
解释：如下面简图所示：
   2
  3 4
 6 5 7
4 1 8 3
自顶向下的最小路径和为 11（即，2 + 3 + 5 + 1 = 11）

示例 2：

输入：triangle = [[-10]]
输出：-10

分析

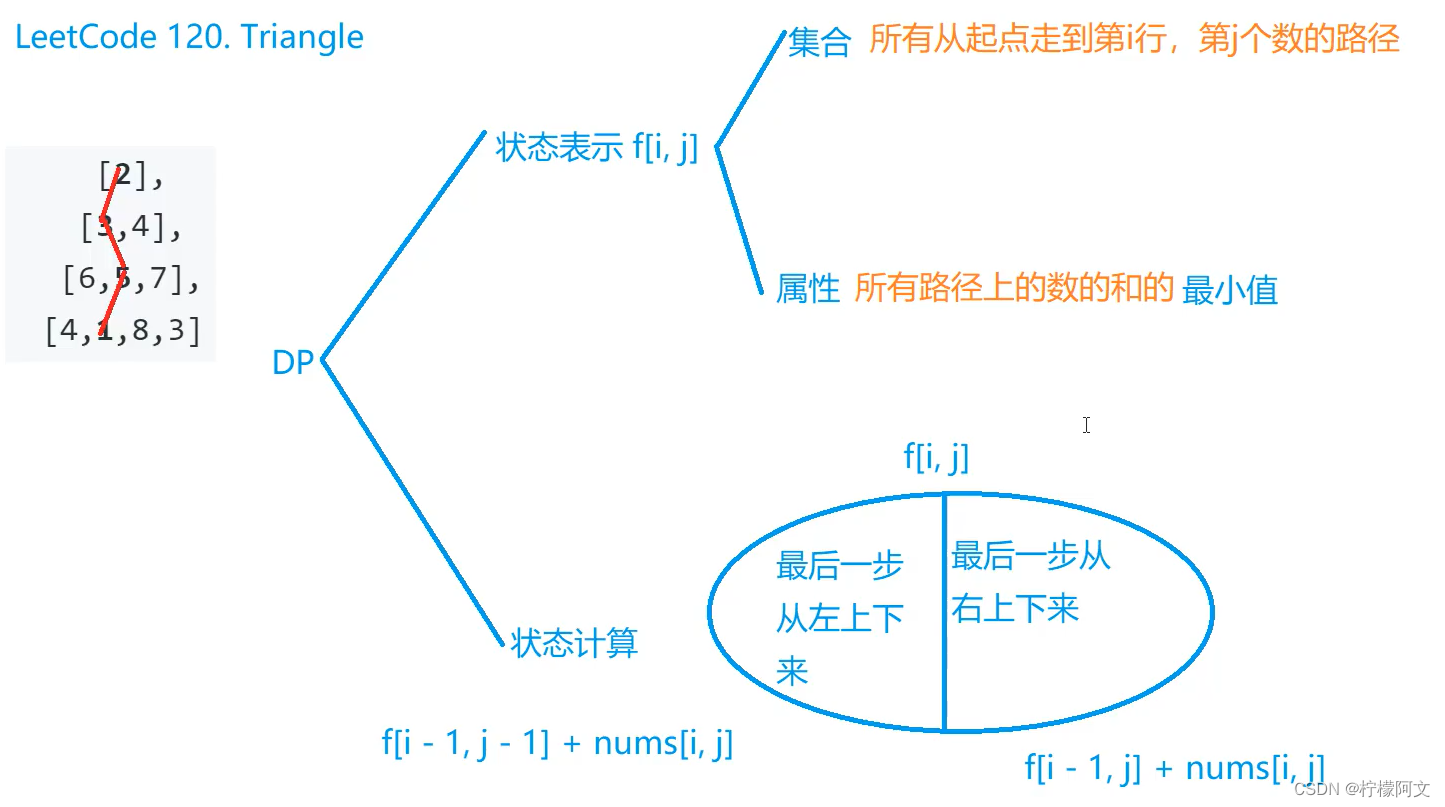
注意：

f[i,j]里面包含两种情况，两种情况不一定全部都包含， 分两种情况，但两种情况也不是全部都在的：
例如三角形的最左边，不可能从左上下来，三角形的最右面，不可能从右上下来。

代码

class Solution {
    public int minimumTotal(List<List<Integer>> triangle) {
        int n = triangle.size();
        int dp[][] = new int[n][n];
        dp[0][0] = triangle.get(0).get(0);
        int res = Integer.MAX_VALUE;
        for (int i = 1;i<n;i++){
            for (int j = 0;j<triangle.get(i).size();j++){
                dp[i][j] = Integer.MAX_VALUE;
                //从左上方来，但是三角形的最左边不可能从左上来
                if (j>0) dp[i][j] = Math.min(dp[i-1][j-1]+triangle.get(i).get(j),dp[i][j]);
                //从右上方来，但是三角形的最右面不可能从右上方来
                if (j<i) dp[i][j] = Math.min(dp[i-1][j]+triangle.get(i).get(j), dp[i][j]);
            }
        }
        //从最后一行中，选择一个最小的路径
        for (int i = 0;i<triangle.size();i++){
            res = Math.min(res,dp[triangle.size()-1][i]);
        }
        return res;
    }
}