回溯法
解决一个回溯问题,实际上就是一个决策树的遍历过程。只需要思考 3 个问题:
1、路径:也就是已经做出的选择。
2、选择列表:也就是你当前可以做的选择。
3、结束条件:也就是到达决策树底层,无法再做选择的条件。
全排列
形式一:不包含重复数字,不可以重复选择的框架
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| private static List<LinkedList<Integer>> res = new LinkedList<>();
public static void way(LinkedList<Integer> list,int nums[]){
if (list.size()==nums.length()){
res.add(new LinkedList<>(list));
return;
}
for (int i = 0;i<n;i++){
if (list.contains(nums[i])) continue;
list.add(nums[i]);
way(list,nums);
list.removeLast();
}
}
|
我们不妨把这棵树称为回溯算法的「决策树」。
为啥说这是决策树呢,因为你在每个节点上其实都在做决策。
可以把「路径」和「选择列表」作为决策树上每个节点的属性,比如下图列出了几个节点的属性:
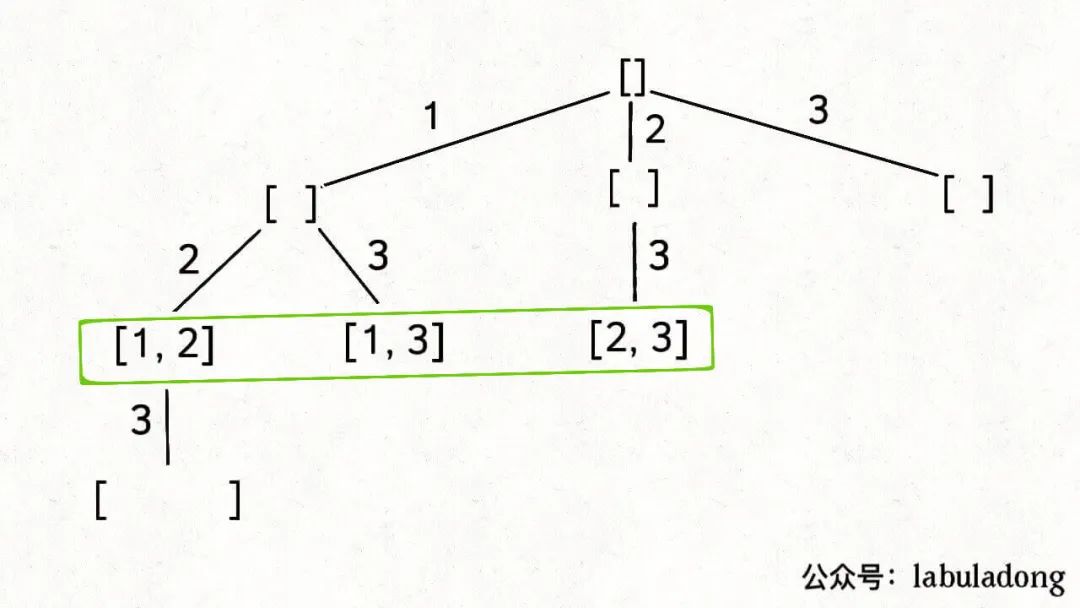
我们只要在递归之前做出选择,在递归之后撤销刚才的选择,就能正确得到每个节点的选择列表和路径。

下面直接看全排列的代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| List<List<Integer>> res = new LinkedList<>();
List<List<Integer>> permute(int[] nums) {
LinkedList<Integer> track = new LinkedList<>();
backtrack(nums, track);
return res;
}
void backtrack(int[] nums, LinkedList<Integer> track) {
if (track.size() == nums.length) {
res.add(new LinkedList(track));
return;
}
for (int i = 0; i < nums.length; i++) {
if (track.contains(nums[i]))
continue;
track.add(nums[i]);
backtrack(nums, track);
track.removeLast();
}
}
|
形式二:包含重复数字,不可重复选择的框架
先将数组排序,让相等的元素靠在一起。
在回溯的循环里面,多一个条件,就是判断当前的元素是否和前一个元素相等,并且前一个元素已经被选择完成。
代码为:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| private static List<LinkedList<Integer>> res = new LinkedList<>();
Arrays.sort(nums);
used = new boolean[nums.length];
public static void way(LinkedList<Integer> list,int nums[]){
if (list.size()==nums.length()){
res.add(new LinkedList<>(list));
return;
}
for (int i = 0;i<n;i++){
if (used[i]) continue;
if (i>0 && nums[i]==nums[i-1] && !used[i - 1]) continue;
list.add(nums[i]);
used[i] = true;
way(list,nums);
list.removeLast();
used[i] = false;
}
}
|
形式三:没有重复,可以重复选择
这个相对简单,没有判断是否选择的条件
代码为:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| private static List<LinkedList<Integer>> res = new LinkedList<>();
public static void way(LinkedList<Integer> list,int nums[]){
if (list.size()==nums.length()){
res.add(new LinkedList<>(list));
return;
}
for (int i = 0;i<n;i++){
list.add(nums[i]);
way(list,nums);
list.removeLast();
}
}
|
形式四:有重复,可以重复选择
既然可以重复选择,则有没有重复元素则没有意义。
将数组去重后,和形式三一样
N皇后问题
可以直接套用代码模板解答
代码为:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
| class Solution {
private List<List<String>> res = new ArrayList<>();
public List<List<String>> solveNQueens(int n) {
char bord[][] = new char[n][n];
for (int i = 0;i<n;i++){
for (int j = 0;j<n;j++){
bord[i][j] = '.';
}
}
just(0,n,bord);
return res;
}
public List<String> arrToList(char bord[][]){
List<String> s = new ArrayList<>();
for (int i = 0;i<bord.length;i++){
StringBuffer str = new StringBuffer();
for (int j = 0;j<bord[0].length;j++){
str.append(bord[i][j]);
}
s.add(str.toString());
}
return s;
}
public void just(int row, int n,char bord[][]){
if (row==n){
res.add(arrToList(bord));
return;
}
for (int col = 0;col<n;col++){
if (!Vaild(row,col,bord)){
continue;
}
bord[row][col] = 'Q';
just(row+1,n,bord);
bord[row][col] = '.';
}
}
public boolean Vaild(int row,int col,char bord[][]){
int n = bord.length;
for (int i = 0;i<n;i++){
if (bord[i][col]=='Q') return false;
}
for (int i = row-1,j = col+1;i>=0 && j<n;i--,j++){
if (bord[i][j] =='Q') return false;
}
for (int i = row-1,j = col-1;i>=0 && j>=0;i--,j--){
if (bord[i][j]=='Q') return false;
}
return true;
}
}
|
子集
给出一个数组,返回数组中所有元素的子集。
比如输入nums = [1,2,3],算法应该返回如下子集:
1
| [ [],[1],[2],[3],[1,2],[1,3],[2,3],[1,2,3] ]
|
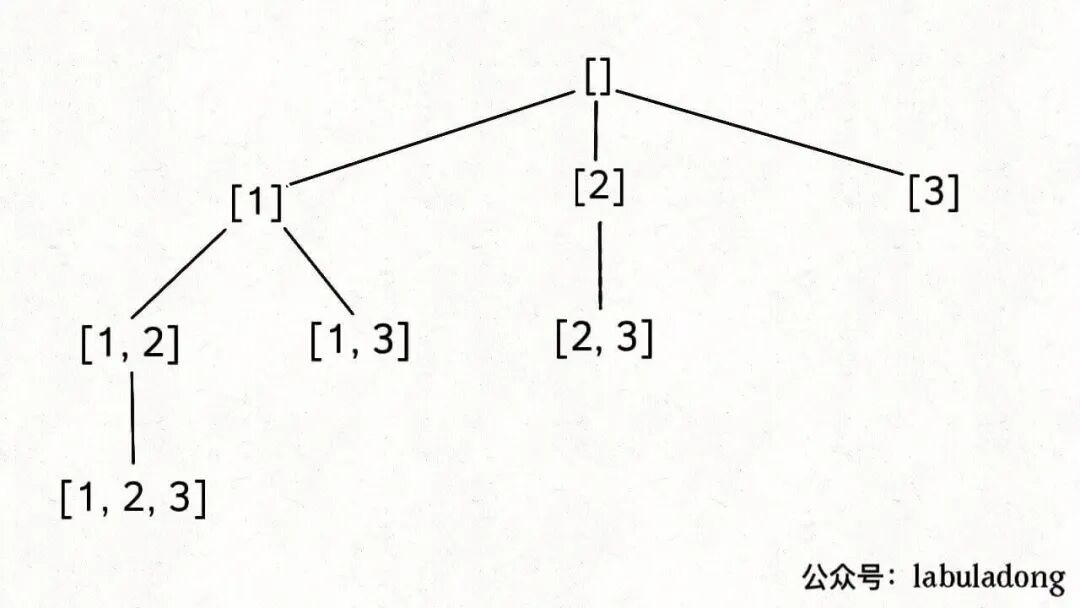
形式一:无重复,不可重复选择
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| public class testgather {
private static List<List<Integer>> res = new ArrayList<>();
private static LinkedList<Integer> list = new LinkedList<>();
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int nums[] = new int[n];
for (int i = 0;i<n;i++) {
nums[i] = scanner.nextInt();
}
gather(0,nums);
System.out.println(res.toString());
}
public static void gather(int start, int nums[]){
res.add(new ArrayList<>(list));
for (int i = start;i<nums.length;i++){
list.add(nums[i]);
gather(i+1,nums);
list.removeLast();
}
}
}
|
形式二:元素重复,不可重复选择
比如输入nums = [1,2,2],你应该输出:
1
| [ [],[1],[2],[1,2],[2,2],[1,2,2] ]
|

1
2
3
4
5
6
| [
[],
[1],[2],[2'],
[1,2],[1,2'],[2,2'],
[1,2,2']
]
|
里面有重复的集合,所以要进行剪枝。
体现在代码上,需要先进行排序,让相同的元素靠在一起,如果发现nums[i] == nums[i-1],则跳过:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| public class testgather {
private static List<List<Integer>> res = new ArrayList<>();
private static LinkedList<Integer> list = new LinkedList<>();
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int nums[] = new int[n];
for (int i = 0;i<n;i++) {
nums[i] = scanner.nextInt();
}
Arrays.sort(nums);
gather(0,nums);
System.out.println(res.toString());
}
public static void gather(int start, int nums[]){
res.add(new ArrayList<>(list));
for (int i = start;i<nums.length;i++){
if (i>start && nums[i]==nums[i-1]) continue;
list.add(nums[i]);
gather(i+1,nums);
list.removeLast();
}
}
}
|
形式三:没有重复,但可以重复选择
比如输入candidates = [1,2,3], target = 3,算法应该返回:
首先来看,怎么样的实现使得不可以重复选择,
在于递归函数是输入的参数,
1
2
3
4
5
6
7
|
for (int i = start; i < nums.length; i++) {
backtrack(nums, i + 1, target);
}
|
这个i从start开始,那么下一层回溯树就是从start + 1开始,从而保证nums[start]这个元素不会被重复使用:
那么反过来,如果我想让每个元素被重复使用,我只要把i + 1改成i即可:
1
2
3
4
5
6
7
|
for (int i = start; i < nums.length; i++) {
backtrack(nums, i, target);
}
|

当然,这样这棵回溯树会永远生长下去,即路径和大于target时就没必要再遍历下去了。
代码为:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
| public class testjihe {
private static List<List<Integer>> res = new ArrayList<>();
private static LinkedList<Integer> list = new LinkedList<>();
private static int sum = 0;
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int nums[] = new int[n];
for (int i = 0;i<n;i++) {
nums[i] = scanner.nextInt();
}
int target = scanner.nextInt();
gather(0,nums,target);
System.out.println(res.toString());
}
public static void gather(int start, int nums[], int target){
if (sum==target){
res.add(new ArrayList<>(list));
return;
}
if (sum>target) return;
for (int i = start;i<nums.length;i++){
sum = sum + nums[i];
list.add(nums[i]);
gather(i,nums,target);
sum = sum-nums[i];
list.removeLast();
}
}
}
|
组合
如果你能够成功的生成所有无重子集,那么你稍微改改代码就能生成所有无重组合了。
因此集合和子集是相同的
给定两个整数n和k,返回范围[1, n]中所有可能的k个数的组合。
函数签名如下:
1
| List<List<Integer>> combine(int n, int k)
|
比如combine(3, 2)的返回值应该是:
这是标准的组合问题,但换一种说就成了子集,
给你输入一个数组nums = [1,2..,n]和一个正整数k,请你生成所有大小为k的子集。

代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| public class testCom {
private static List<List<Integer>> res = new ArrayList<>();
private static LinkedList<Integer> list = new LinkedList<>();
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int k = scanner.nextInt();
com(1,n,k);
System.out.println(res.toString());
}
public static void com(int a,int n,int k){
if (k== list.size()){
res.add(new LinkedList<>(list));
return;
}
for (int i = a;i<=n;i++){
list.add(i);
com(i+1,n,k);
list.removeLast();
}
}
}
|
组合和子集相同,可以直接看子集。
框架总结
形式一、元素无重不可复选
即nums中的元素都是唯一的,每个元素最多只能被使用一次,backtrack核心代码如下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
void backtrack(int[] nums, int start) {
res.add(new ArrayList<>(list));
for (int i = start; i < nums.length; i++) {
track.addLast(nums[i]);
backtrack(nums, i + 1);
track.removeLast();
}
}
void backtrack(int[] nums) {
for (int i = 0; i < nums.length; i++) {
if (used[i]) {
continue;
}
used[i] = true;
track.addLast(nums[i]);
backtrack(nums);
track.removeLast();
used[i] = false;
}
}
|
形式二、元素可重不可复选
即nums中的元素可以存在重复,每个元素最多只能被使用一次,其关键在于排序和剪枝,backtrack核心代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
| Arrays.sort(nums);
void backtrack(int[] nums, int start) {
res.add(new ArrayList<>(list));
for (int i = start; i < nums.length; i++) {
if (i > start && nums[i] == nums[i - 1]) {
continue;
}
track.addLast(nums[i]);
backtrack(nums, i + 1);
track.removeLast();
}
}
Arrays.sort(nums);
void backtrack(int[] nums) {
for (int i = 0; i < nums.length; i++) {
if (used[i]) {
continue;
}
if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) {
continue;
}
used[i] = true;
track.addLast(nums[i]);
backtrack(nums);
track.removeLast();
used[i] = false;
}
}
|
形式三、元素无重可复选
即nums中的元素都是唯一的,每个元素可以被使用若干次,只要删掉去重逻辑即可,backtrack核心代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
void backtrack(int[] nums, int start) {
res.add(new ArrayList<>(list));
for (int i = start; i < nums.length; i++) {
track.addLast(nums[i]);
backtrack(nums, i);
track.removeLast();
}
}
void backtrack(int[] nums) {
for (int i = 0; i < nums.length; i++) {
track.addLast(nums[i]);
backtrack(nums);
track.removeLast();
}
}
|