模板2-数据结构

链表

单链表

使用数组来进行单链表的操作、

模板：

static int N = 100010;
   static int e[] = new int[N];  //e[i]:下标为i的节点的值
   static int ne[] = new int[N];  //ne[i]:下标为i的节点的下一个节点
   static int idx;  //表示当前用到了哪个节点
   static int head;//头节点

   //初始化
   public static void init(){
       head = -1;
       idx = 0;
   }


   //插入头节点
   public static void addHead(int a){
       e[idx] = a;
       ne[idx] = head;
       head = idx;
       idx++;
   }

   //将a插入到下标是k节点的后面
   public static void add(int k,int a){
       e[idx] = a;
       ne[idx] = ne[k];
       ne[k] = idx;
       idx++;
       
   }

   //删除下标为k的下一个节点
   public static void remove(int k){
       ne[k] = ne[ne[k]];
   }

例题：

代码为：

import java.util.*;
import java.io.*;
public class Main{
    static int N = 100010;
    static int e[] = new int[N];  //e[i]:下标为i的节点的值
    static int ne[] = new int[N];  //ne[i]:下标为i的节点的下一个节点
    static int idx;  //表示当前用到了哪个节点
    static int head;//头节点

    //初始化
    public static void init(){
        head = -1;
        idx = 0;
    }

    //插入头节点
    public static void addHead(int a){
        e[idx] = a;
        ne[idx] = head;
        head = idx;
        idx++;
    }

    //将a插入到下标是k节点的后面
    public static void add(int k,int a){
        e[idx] = a;
        ne[idx] = ne[k];
        ne[k] = idx;
        idx++;
    }

    //删除下标为k的下一个节点
    public static void remove(int k){
        ne[k] = ne[ne[k]];
    }

    public static void main(String[] args) throws Exception {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        PrintWriter pw =  new PrintWriter(new BufferedWriter(new OutputStreamWriter(System.out)));
        int n = Integer.parseInt(br.readLine()) ;//操作次数
        init();
        while (n-->0){
            String s[] = br.readLine().split(" ");
            char p = s[0].charAt(0);
            if (p=='H'){
                int a = Integer.parseInt(s[1]);
                addHead(a);
            }else if (p=='D'){
                int k = Integer.parseInt(s[1]);
                if (k==0) head = ne[head];
                else remove(k-1);
            }else {
                int k = Integer.parseInt(s[1]);
                int a = Integer.parseInt(s[2]);
                add(k-1,a);
            }
        }
        for (int i = head;i!=-1;i=ne[i]){
            pw.print(e[i]+" ");
        }
        pw.flush();
    }
}

双链表

模板;

//初始化
    public static void init(){
        //0:表示头节点，1:表示尾节点
        r[0] = 1; //左端点的右边是1
        l[1] = 0; //右端点的左边是0
        idx = 2;
    }
    //在第k位数的面右边添加节点
    //在第k位数的左边添加，也可以用这个，(l[k],a),变成了，在l[k]的右边添加节点
    public static void add(int k,int a){
        e[idx] = a;
        l[idx] = k;
        r[idx] = r[k];
        l[r[k]] = idx;
        r[k] = idx;
        idx++;
    }
    //删除第k个插入的数
    public static void delete(int k){
        l[r[k]] = l[k];
        r[l[k]] = r[k];
    }

例题：

代码为：

import java.io.*;
import java.util.*;
public class Main{
    static int N = 100010;
    static int e[] = new int[N];
    static int l[] = new int[N];
    static int r[] = new int[N];
    static int idx;
    //初始化
    public static void init(){
        //0:表示头节点，1:表示尾节点
        r[0] = 1; //左端点的右边是1
        l[1] = 0; //右端点的左边是0
        idx = 2;
    }
    //在第k位数的面右边添加节点
    //在第k位数的左边添加，也可以用这个，(l[k],a),变成了，在l[k]的右边添加节点
    public static void add(int k,int a){
        e[idx] = a;
        l[idx] = k;
        r[idx] = r[k];
        l[r[k]] = idx;
        r[k] = idx;
        idx++;
    }
    //删除第k个插入的数
    public static void delete(int k){
        l[r[k]] = l[k];
        r[l[k]] = r[k];
    }

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        PrintWriter pw = new PrintWriter(new BufferedWriter(new OutputStreamWriter(System.out)));
        init();
        int n = Integer.parseInt(br.readLine());
        while (n-->0){
            String s[] = br.readLine().split(" ");
            String op = s[0];
            if (op.equals("D")){
                int k = Integer.parseInt(s[1]);
                delete(k+1);
            }else if (op.equals("IL")){
                int k = Integer.parseInt(s[1]);
                int a = Integer.parseInt(s[2]);
                add(l[k+1],a);  //因为初始化的时候，加了两个点，所以，第k个数的下标为 ：k+2-1=k+1
            }else if (op.equals("IR")){
                int k = Integer.parseInt(s[1]);
                int a = Integer.parseInt(s[2]);
                add(k+1,a);
            }else if (op.equals("L")){
                int a = Integer.parseInt(s[1]);
                add(0,a);//也就是相当于头节点的右端
            }else if (op.equals("R")){
                int a = Integer.parseInt(s[1]);
                add(l[1],a);
            }
        }
        for (int i = r[0];i!=1;i=r[i]){
            System.out.print(e[i]+" ");
        }
    }
}

栈

数组模拟栈的插入，弹出，是否为空，查询栈顶元素、

模板：

static int N = 100010;
static int a[] = new int[N];
static int t = 0;
//在栈中添加元素
public static void push(int x){
    a[++t] = x;
}
//弹出栈顶的元素
public static void pop(){
    if (t>0) {
        --t;
    }
}
//判断栈是否为空
public static String isEmpty(){
    if (t==0) return "YES";
    else return "NO";
}
//查询栈顶元素
public static int query(){
    return a[t];
}

表达式求值也使用了栈的数据结构，就是给出一个字符串的表达式，求出计算结果，详细的请见，表达式求值那个文章。

单调栈

运用的场景：

• 给定一个序列，求在这个序列中，每个数的左边（或右边），离它最近的（比它大或小）的数在什么地方。

模板为“：

for (int i = 0;i<n;i++){
    int t = scanner.nextInt();
    //如果栈不为空，并且栈顶元素大于目前遍历到的元素，则删除栈顶
    while (tt!=0 && a[tt]>=t) tt--;
    //如果栈不为空，说明在栈中找到了比该元素小的元素，进行输出
    if (tt!=0) System.out.print(a[tt]+" ");
    //如果最后栈为空，说明之前没有比它小数，输出-1
    else System.out.print(-1+" ");
    a[++tt] = t;
}
//该元素右边离它最近比它大的数
Map<Integer,Integer> map = new HashMap<>();
Deque<Integer> deque = new ArrayDeque<>();
int len1 = nums1.length;
int len2 = nums2.length;
for (int i = len2-1;i>=0;i--){
	int t = nums2[i];
	while (!deque.isEmpty() && deque.peek()<=t) deque.pop();
	if (!deque.isEmpty()) {
		map.put(t,deque.peek());
	}else {
		map.put(t,-1);
	}
	deque.push(t);
}

例题：

代码为：

import java.util.*;
public class Main{
    static int N = 100010;
    static int a[] = new int[N];
    public static void main(String[] args) {
        int tt = 0;
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();
        for (int i = 0;i<n;i++){
            int t = scanner.nextInt();
            //如果栈不为空，并且栈顶元素大于目前遍历到的元素，则删除栈顶
            while (tt!=0 && a[tt]>=t){
                tt--;
            }
            //如果栈不为空，说明在栈中找到了比该元素小的元素，进行输出
            if (tt!=0) System.out.print(a[tt]+" ");
            //如果最后栈为空，说明之前没有比它小数，输出-1
            else System.out.print(-1+" ");
            a[++tt] = t;
        }
    }
}

队列

数组模拟队列

模板：

  int hh = 0,tt = -1;
//队尾插入
   public static void add(int a){
       q[++tt] = a;
   }
   //队头弹出
   public static void pop(){
       hh++;
   }
   //判断是否为空
   public static String isEmpty(){
       if (hh<=tt) return "NO";
       else return "YES";
   }
   //查询队头元素
   public static int query(){
       return q[hh];
   }

单调队列

应用场景

• 求滑动窗口里面的最大值或最小值。

最大值和最小值分开来做，两个for循环搞定。步骤为：

• 解决队首已经出窗口的问题;
• 解决队尾与当前元素a[i]不满足单调性的问题;
• 将当前元素下标加入队尾;
• 如果满足条件则输出结果;

模板”：

int hh = 0;int tt = -1;
//最小值
for (int i = 0;i<n;i++){
    //解决队首已经出窗口的问题
    if (hh<=tt && i-q+1>queue[hh]) hh++;
    //解决队尾与当前元素a[i]不满足单调性的问题，也就是要插入的元素是否小于队顶元素，如果小于，则删除队顶元素
	while (hh<=tt && a[queue[tt]]>=a[i]) tt--;
    //将当前元素下标加入队尾
    queue[++tt] = i;
    //如果满足条件则输出结果：i 必须满足滑动窗口的条件
    if (i>=q-1) pw.print(a[queue[hh]]+" ");
}
pw.println();

//最大值
hh = 0;tt = -1;
for (int i = 0;i<n;i++){
    if (hh<=tt && i-q+1>queue[hh]) hh++;
	while (hh<=tt && a[queue[tt]] <= a[i]) tt--;
    queue[++tt] = i;
    if (i>=q-1) pw.print(a[queue[hh]]+" ");
}

例题：

给定一个大小为 n≤10的6次幂的数组。有一个大小为 k 的滑动窗口，它从数组的最左边移动到最右边。你只能在窗口中看到 k 个数字。每次滑动窗口向右移动一个位置。求滑动窗口中的最小值和最大值：

输入样例：

8 3
1 3 -1 -3 5 3 6 7

输出样例：

-1 -3 -3 -3 3 3
3 3 5 5 6 7

代码为：

import java.util.*;
import java.io.*;
public class Main{
    static int N = 1000010;
    static int a[] = new int[N];
    static int queue[] = new int[N];
    public static void main(String[] args) throws Exception {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        PrintWriter pw = new PrintWriter(new BufferedWriter(new OutputStreamWriter(System.out)));
        String s[] = br.readLine().split(" ");
        int n = Integer.parseInt(s[0]);
        int q = Integer.parseInt(s[1]);
        String ss[] = br.readLine().split(" ");
        for (int i = 0;i<n;i++){
            a[i] = Integer.parseInt(ss[i]);
        }
        int hh = 0;int tt = -1;
        //最小值
        for (int i = 0;i<n;i++){
            if (hh<=tt && i-q+1>queue[hh]){
                hh++;
            }
            while (hh<=tt && a[queue[tt]]>=a[i]) tt--;
            queue[++tt] = i;
            if (i>=q-1) pw.print(a[queue[hh]]+" ");
        }
        pw.println();
        //最大值
        hh = 0;tt = -1;
        for (int i = 0;i<n;i++){
            if (hh<=tt && i-q+1>queue[hh]){
                hh++;
            }
            while (hh<=tt && a[queue[tt]] <= a[i]) tt--;
            queue[++tt] = i;
            if (i>=q-1) pw.print(a[queue[hh]]+" ");
        }
        pw.flush();
    }
}

KMP算法

没弄懂，，背就完了

模板：

//模式串s，模板串p 	
//next数组
 for(int i = 2 , j = 0; i  <= pn ; i ++ ){
     while(j > 0 && p[i] != p[j+1]) j = ne[j];
     if(p[i] == p[j+1]) j ++ ;
     ne[i] = j;
 }

 //匹配过程
 for(int i = 1 ,j = 0 ; i <= sm ; i ++ ){
     while(j > 0 && s[i] != p[j+1]) j = ne[j];
     if(s[i] == p[j+1]) j++;
     if(j == pn){
         pw.write((i - pn) + " ");
         j = ne[j];
     }
 }

例题：

代码为：

import java.io.*;
import java.util.*;
public class Main{
    static int N = 100010;
    static int M = 1000010;
    static int ne[] = new int[N];
    static char s[] = new char[M];
    static char p[] = new char[N];
    public static void main(String[] args) throws Exception {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        PrintWriter pw = new PrintWriter(new BufferedWriter(new OutputStreamWriter(System.out)));
        int pn = Integer.parseInt(br.readLine()); //短
        String pp = br.readLine();
        for (int i = 1;i<=pn;i++){
            p[i] = pp.charAt(i-1);
        }
        int sm = Integer.parseInt(br.readLine()); //长
        String ss = br.readLine();
        for (int i = 1;i<=sm;i++){
            s[i] = ss.charAt(i-1);
        }
        
       //next数组
        for(int i = 2 , j = 0; i  <= pn ; i ++ ){
            while(j > 0 && p[i] != p[j+1]) j = ne[j];
            if(p[i] == p[j+1]) j ++ ;
            ne[i] = j;
        }


        //匹配过程
        for(int i = 1 ,j = 0 ; i <= sm ; i ++ ){
            //判断j是不是大于0，小于=0表示还没有前缀和后缀相等
            //判断长的数组一个一个遍历比较，看看短的数组，如果不相等就让j = 上一个数的缀长度
            while(j > 0 && s[i] != p[j+1]) j = ne[j];
            //如果相等就让j++；继续进行下一个数的比较
            if(s[i] == p[j+1]) j++;
            //如果相等的数等于短的数组的长度，就说明该输出了
            if(j == pn){
                pw.write((i - pn) + " ");
                //输出之后，要继续往下面遍历对比，所以让j=上一个数的缀长度，
                //因为有前缀和后缀相等的部分可以重复使，并且相同的位置不止一个
                j = ne[j];
            }
        }
        pw.flush();
    }
}

Trie树

Trie树又称字典树、单词查找树。是一种能够高效存储和查找字符串集合的数据结构。

存储字符串：

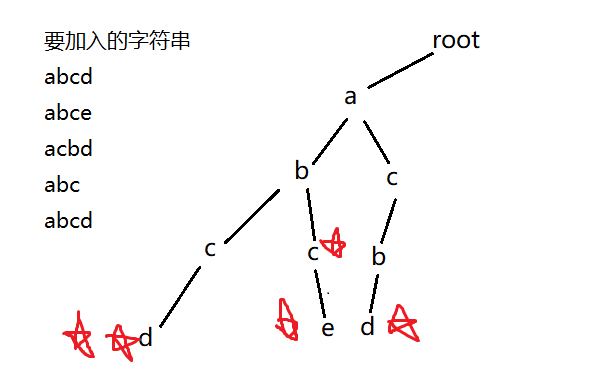
Trie树的代码具体分析：

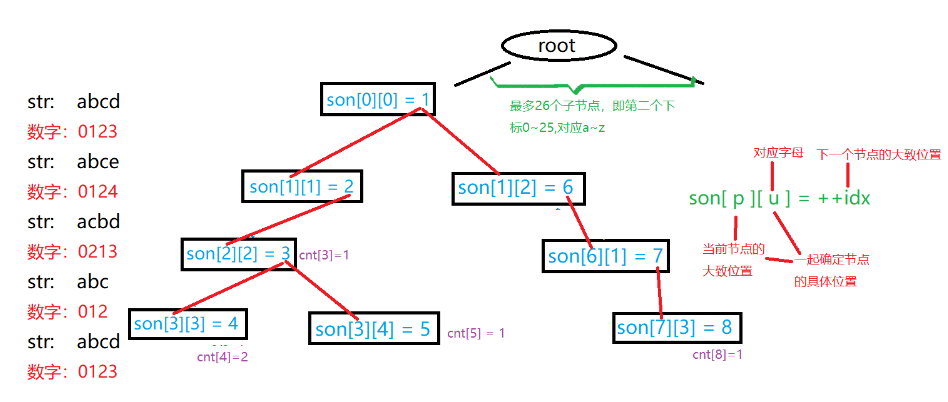
模板代码“：

static int N = 10010;
   static int son[][] = new int[N][26];//当前节点儿子
   static int cnt[] = new int[N];  //cnt[p]：以p为结尾的字符串的个数
   static int idx = 0;  //当前节点
   //插入
   public static void insert(String s){
       int len = s.length();
       int p = 0;  //指向当前的节点
       for (int i = 0;i<len;i++){
           int u = s.charAt(i)-'a'; //将字母转化为数字
           if (son[p][u]==0) son[p][u] = ++idx; //节点不存在的时候，创建该节点，值为下一个节点的位置
           p = son[p][u]; //p指向下一个节点
       }
       cnt[p]++;//结束的标记，记录以此节点结束的字符串个数
   }
   //询问
   public static void query(String s){
       int len = s.length();
       int p = 0;
       for (int i = 0;i<len;i++){
           int u = s.charAt(i)-'a';
           if (son[p][u]==0){  //如果为0 说明该节点不存在，直接输出0
               System.out.println(0);
               return;
           }
           p = son[p][u];  
       }
       System.out.println(cnt[p]); //输出字符串出现的次数
   }

例题;

代码为：

import java.util.*;
import java.io.*;
public class Main{
    static int N = 10010;
    static int son[][] = new int[N][26];
    static int cnt[] = new int[N];
    static int idx = 0;
    //插入
    public static void insert(String s){
        int len = s.length();
        int p = 0;
        for (int i = 0;i<len;i++){
            int u = s.charAt(i)-'a';
            if (son[p][u]==0) son[p][u] = ++idx;
            p = son[p][u];
        }
        cnt[p]++;
    }
    //询问
    public static void query(String s){
        int len = s.length();
        int p = 0;
        for (int i = 0;i<len;i++){
            int u = s.charAt(i)-'a';
            if (son[p][u]==0){
                System.out.println(0);
                return;
            }
            p = son[p][u];
        }
        System.out.println(cnt[p]);
    }

    public static void main(String[] args) throws Exception {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int n = Integer.parseInt(br.readLine());
        while (n-->0){
            String p[] = br.readLine().split(" ");
            if (p[0].equals("I")) insert(p[1]);
            else if (p[0].equals("Q")) {
                query(p[1]);
            }
        }
    }
}

并查集

在上述的问题中，问题2的时间复杂度较高，因为遍历集合编号，只要是和数的高度成正比的，因此每次遍历需要很多的时间复杂度，因此可以进行优化。

路径压缩优化：

代码模板：

一：朴素并查集

static int p[] = new int[N]; //存储每个点的祖宗节点

// 返回x的祖宗节点   find函数重要！！！
public static int find(int x){
    if (p[x]!=x) p[x] = find(p[x]);  //将x的父亲置为x父亲的祖先节点,实现路径的压缩
    return p[x];
}

// 初始化，假定节点编号是1~n
for (int i  =0;i<n;i++){ p[i] = i;}

// 合并a和b所在的两个集合：
p[find(a)] = find(b);

二：维护集合里面元素的个数

static int p[] = new int[N]; //存储每个点的祖宗节点
static int size[] = new int[N];
// 返回x的祖宗节点   find函数重要！！！
public static int find(int x){
    if (p[x]!=x) p[x] = find(p[x]);  //将x的父亲置为x父亲的祖先节点,实现路径的压缩
    return p[x];
}

// 初始化，假定节点编号是1~n
for (int i  =0;i<n;i++){
	p[i] = i;
	size[i] = 1;
}

// 合并a和b所在的两个集合：
if(find(a)!=find(b)) size[find(b)] += size[find(a)];
p[find(a)] = find(b);

连通块：如果可以从A走到B。并且B也可以走到A，就说明A和B在同一个连通块当中的。

三：维护到根节点距离的并查集

int p[N], d[N];
    //p[]存储每个点的祖宗节点, d[x]存储x到p[x]的距离

    // 返回x的祖宗节点
    int find(int x)
    {
        if (p[x] != x)
        {
            int u = find(p[x]);
            d[x] += d[p[x]];
            p[x] = u;
        }
        return p[x];
    }

    // 初始化，假定节点编号是1~n
    for (int i = 1; i <= n; i ++ )
    {
        p[i] = i;
    }

    // 合并a和b所在的两个集合：
    p[find(a)] = find(b);

例题：

代码为：

import java.util.*;
import java.io.*;
public class Main{
    static int N = 100010;
    static int p[] = new int[N];
    public static int find(int x){
        if (p[x]!=x) p[x] = find(p[x]);
        return p[x];
    }
    public static void main(String[] args) throws Exception {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        PrintWriter pw = new PrintWriter(new BufferedWriter(new OutputStreamWriter(System.out)));
        String s[] = br.readLine().split(" ");
        int n = Integer.parseInt(s[0]);
        int m = Integer.parseInt(s[1]);
        for (int i  =0;i<n;i++){
            p[i] = i;
        }
        while (m-->0){
            String ss[] = br.readLine().split(" ");
            if (ss[0].equals("M")){
                int a = Integer.parseInt(ss[1]);
                int b = Integer.parseInt(ss[2]);
                p[find(a)] = find(b);
            }else {
                int a = Integer.parseInt(ss[1]);
                int b = Integer.parseInt(ss[2]);
                if (find(a)==find(b)) pw.println("Yes");
                else pw.println("No");
            }
        }
        pw.flush();
    }
}

例题2：连通块中点的数量

代码为：

import java.util.*;
import java.io.*;
public class Main{
    static int N = 100010;
    static int p[] = new int[N];
    static int size[] = new int[N];
    public static int find(int x){
        if (p[x]!=x) p[x] = find(p[x]);
        return p[x];
    }
    public static void main(String[] args) throws IOException {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();
        int m = scanner.nextInt();
        for (int i = 0;i<n;i++){
            p[i] = i;
            size[i] = 1;
        }
        while (m-->0){
            String ss = scanner.next();
            if (ss.equals("C")) {
                int a = scanner.nextInt();
                int b = scanner.nextInt();
                if (find(a)==find(b)) continue;
                else {
                    size[find(b)] = size[find(b)] + size[find(a)];
                    p[find(a)] = find(b);
                }
            }else if (ss.equals("Q1")){
                int a = scanner.nextInt();
                int b = scanner.nextInt();
                if (find(a)==find(b)){
                    System.out.println("Yes");
                }else {
                    System.out.println("No");
                }
            }else {
                int a = scanner.nextInt();
                System.out.println(size[find(a)]);
            }
        }
    }
}

例题3：

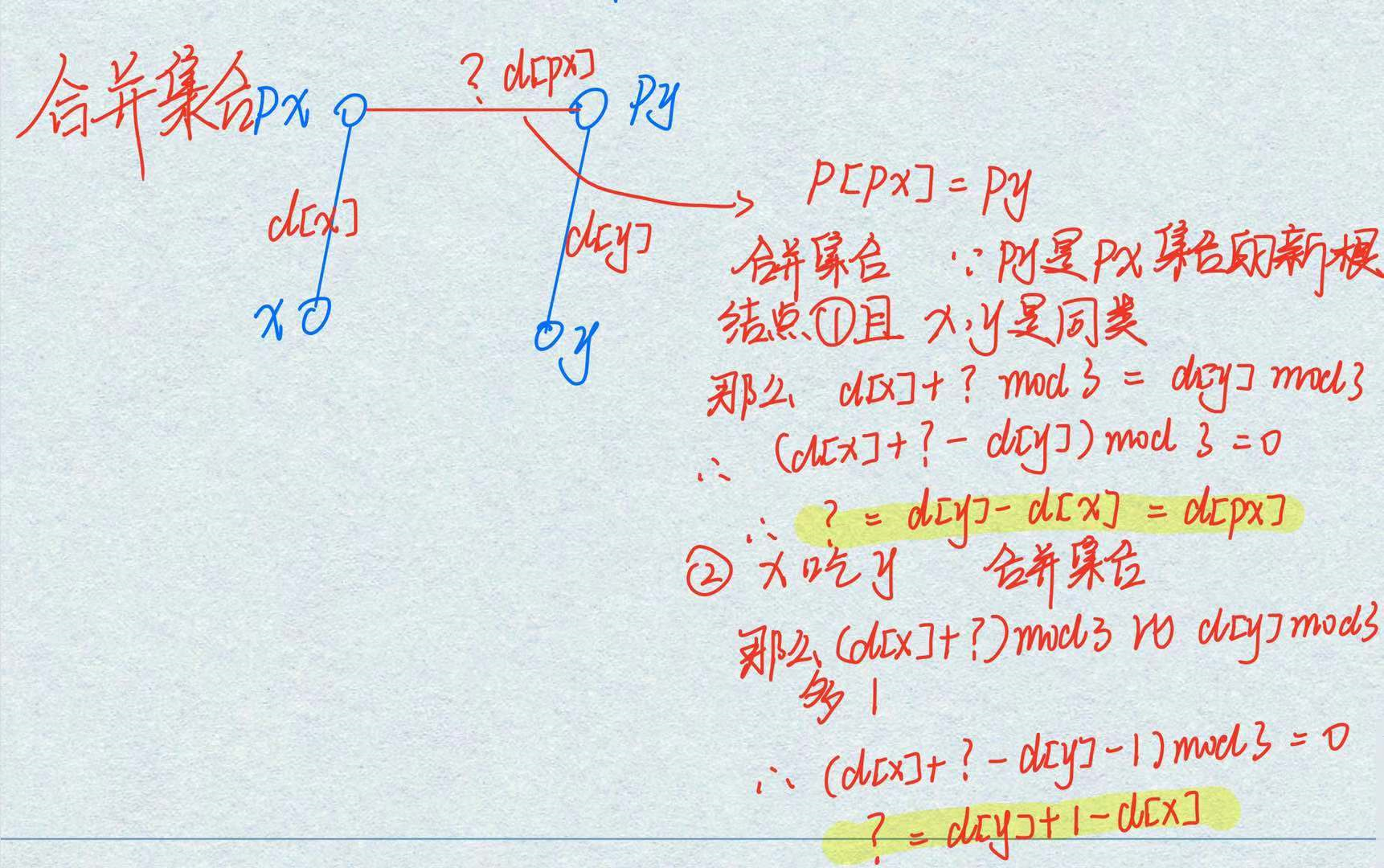
代码为：

import java.util.*;
import java.io.*;
public class Main{
    static int N = 50010;
    static int p[] = new int[N];
    static int d[] = new int[N];  //到根节点的距离
    public static int find(int x){
        if (p[x]!=x){
            int t = find(p[x]);
            d[x] = d[x] + d[p[x]];//计算到根节点的距离
            p[x] = t;
        }
        return p[x];
    }
    public static void main(String[] args) throws Exception {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        PrintWriter pw = new PrintWriter(new BufferedWriter(new OutputStreamWriter(System.out)));
        String s[] = br.readLine().split(" ");
        int n = Integer.parseInt(s[0]);
        int k = Integer.parseInt(s[1]);
        //初始化p
        for (int i = 0;i<n;i++) p[i] = i;
        int res = 0;
        while (k-- >0){
            String s2[] = br.readLine().split(" ");
            int t = Integer.parseInt(s2[0]);
            int a = Integer.parseInt(s2[1]);
            int b = Integer.parseInt(s2[2]);
            if (a>n || b>n) res++;
            else{
                int pa = find(a);
                int pb = find(b);
                if (t==1){//如果是同类的情况下
                    //如果根节点相等，但不是同类则为假话
                    if (pa==pb && (d[a]-d[b])%3!=0) res++;
                    //如果不是一个根节点 则合并，并且设置为同类
                    else if(pa!=pb){
                        p[pa] = pb;
                        //(d[a] + ? - d[b]) % 3 == 0  => ? = db - da 
                        d[pa]  = d[b] - d[a];
                    }
                }else {  //a吃b
                    //a吃b 的条件是a比b大1，
                    if (pa==pb && (d[a]-d[b]-1)%3!=0) res++;
                    else if(pa!=pb){
                        p[pa] = pb;
                        //(da + ? - db - 1) % 3 == 0 =>  ? = db - da + 1
                        d[pa]  = d[b] - d[a] + 1;
                    }
                }
            } 
        }
        pw.println(res);
        pw.flush();
    }
}

堆

其中堆中包含两个操作，一个是down，另一个是up。

down：当修改堆中的数字使其变大的时候，进行down操作，将该节点的根，左子树，右子树，进行比较，如果左右子节点比修改后的小，则与最小的数进行交换，。依次进行这个操作，直到又形成一个堆。

up:当变小一个堆中的数字。进行up操作，与它的根节点进行比较，如果小于根节点，则交换，依次比较。

在数组中，如果根的下标为x，则根的左儿子下标为2x，根的右儿子下标为2x+1。

ph[k] = u:第k个插入的数，在堆中的下标是u；
hp[u] = k:堆中下标为u的，是第k个插入的数；