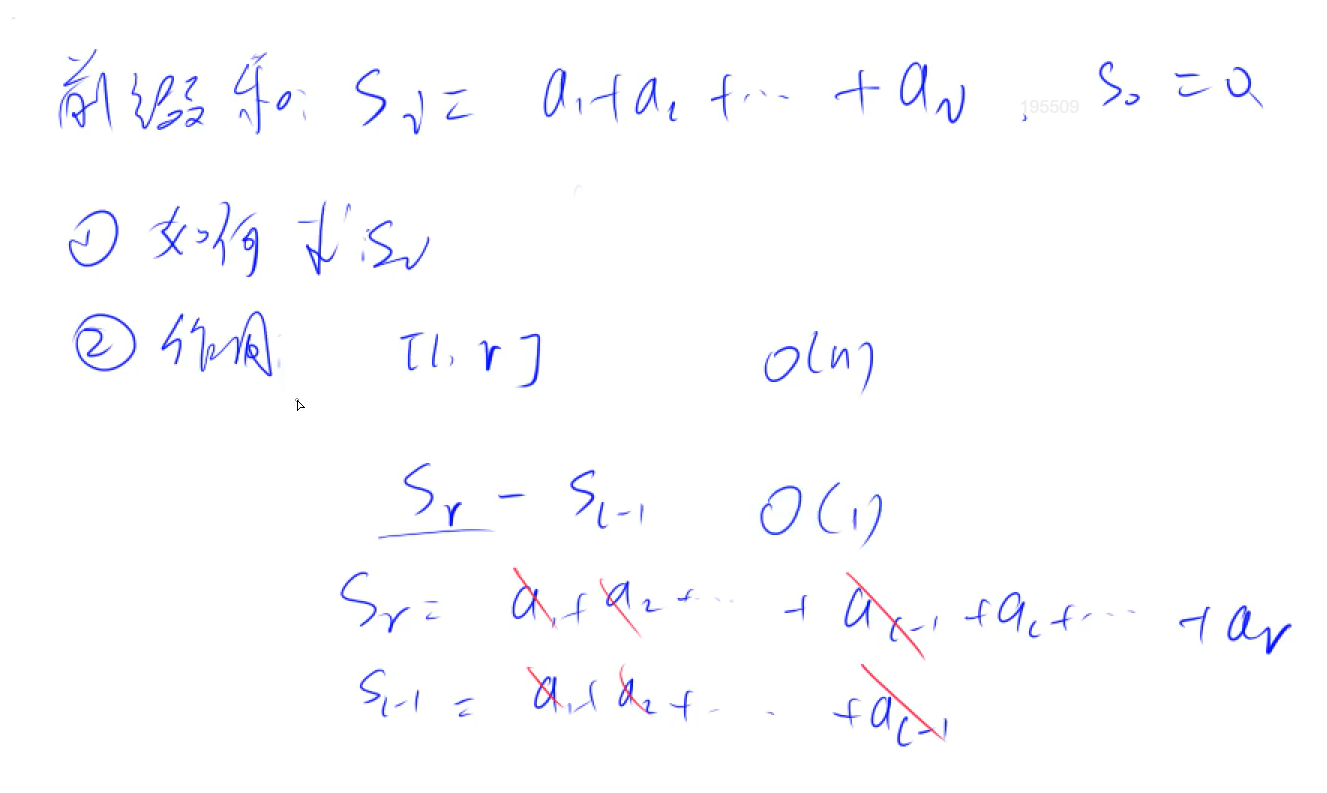模板1-基础算法

前缀和

一维前缀和

计算区间之内的和都可以统一用这个公式：S[r]-S[l-1]

下标必须从1开始，S0 = 0；为了处理边界问题，例如：求[1,10]之间的和：S[10]-S[0]，为了所有的区间都可以使用这个公式，所以下标要从1开始，S0设置为0，因为要用到S0.

1
2
S[i] = a[1] + a[2] + ... a[i]
a[l] + ... + a[r] = S[r] - S[l - 1]

image-20220615220854543

例题：

输入格式

第一行包含两个整数 n 和 m。

第二行包含 n 个整数，表示整数数列。

接下来 m 行，每行包含两个整数 l 和 r，表示一个询问的区间范围。

代码为：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
import java.util.*;
public class Main{
    static int N = 100010;
    static int M = 100010;
    static int a[] = new int[N];
    static int s[] = new int[N];
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();
        int m = scanner.nextInt();
        for (int i = 1;i<=n;i++){
            a[i] = scanner.nextInt();
        }

        for (int i = 1;i<=n;i++){
            s[i] = s[i-1] + a[i]; //求每个数的前缀和
        }
        while (m-->0){
            int l = scanner.nextInt();
            int r = scanner.nextInt();
            System.out.println(s[r]-s[l-1]);  //一维求两个数之间的和
        }
    }
}

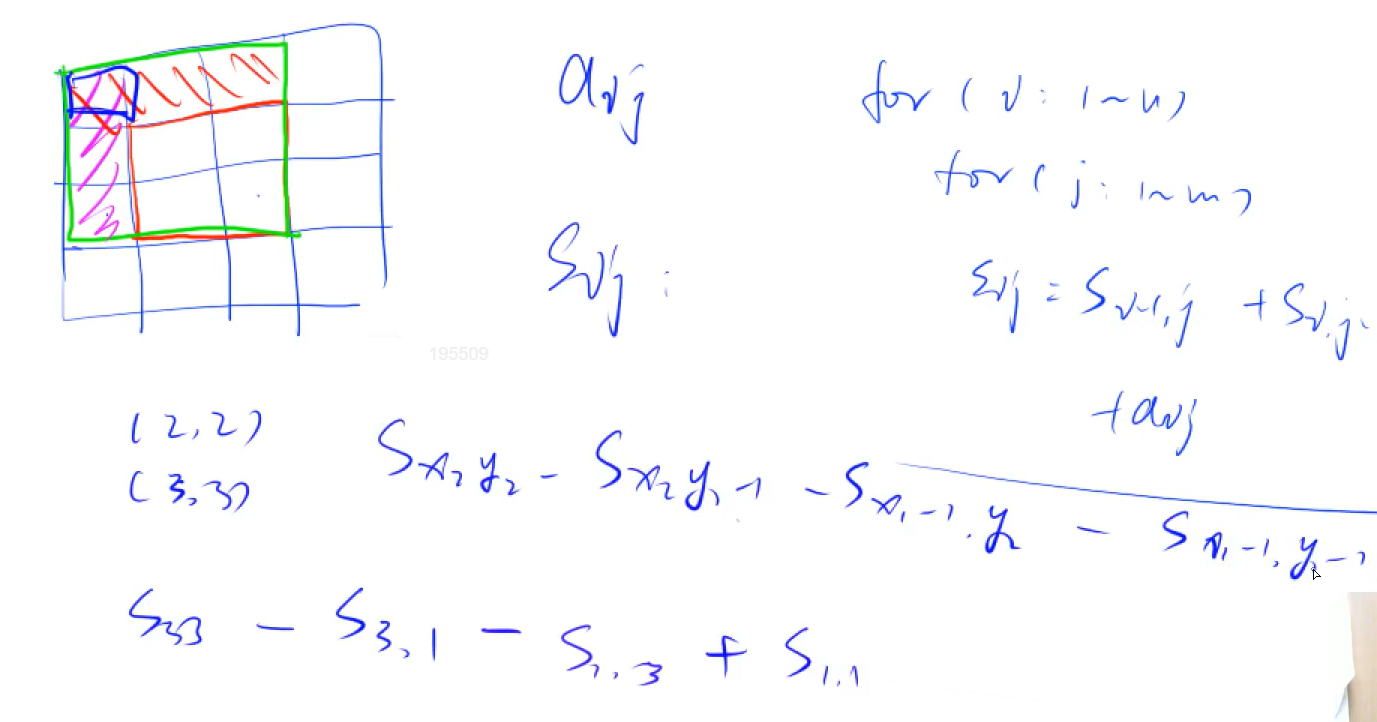
二维前缀和

S[i, j] = 第i行j列格子左上部分所有元素的和
以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵的和为：
S[x2, y2] - S[x1 - 1, y2] - S[x2, y1 - 1] + S[x1 - 1, y1 - 1]

推到：

image-20220616113027318

而其中的S[x,y] = S[x-1,y] + S[x,y-1] - S[x-1,y-1] + a[x,y];

例题：

输入格式

第一行包含三个整数 n，m，q。

接下来 n 行，每行包含 m 个整数，表示整数矩阵。

接下来 q 行，每行包含四个整数 x1,y1,x2,y2,表示一组询问。

代码为：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
import java.io.*;
import java.util.*;
public class Main{
    static int N = 1010;
    static int M = 1010;
    static int Q = 200010;
    static int qq[] = new int[Q];
    static int s[][] = new int[N][M];
    static int a[][] = new int[N][M];
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();//行
        int m = scanner.nextInt();//列
        int q = scanner.nextInt();
        for (int i = 1;i<=n;i++){
            for (int j = 1;j<=m;j++){
                a[i][j] = scanner.nextInt();
            }
        }

        for (int i = 1;i<=n;i++){
            for (int j = 1;j<=m;j++){
                s[i][j] = s[i-1][j] + s[i][j-1] - s[i-1][j-1]+a[i][j]; //先算每个方块中的前缀和，用了上面说的公式
            }
        }
        while (q-->0){
            int x1 = scanner.nextInt();
            int y1 = scanner.nextInt();
            int x2 = scanner.nextInt();
            int y2 = scanner.nextInt();

            int res = s[x2][y2] - s[x1-1][y2] - s[x2][y1-1] + s[x1-1][y1-1];  //两个方块之间的和，用了上面说的公式
            System.out.println(res);
        }

    }
}

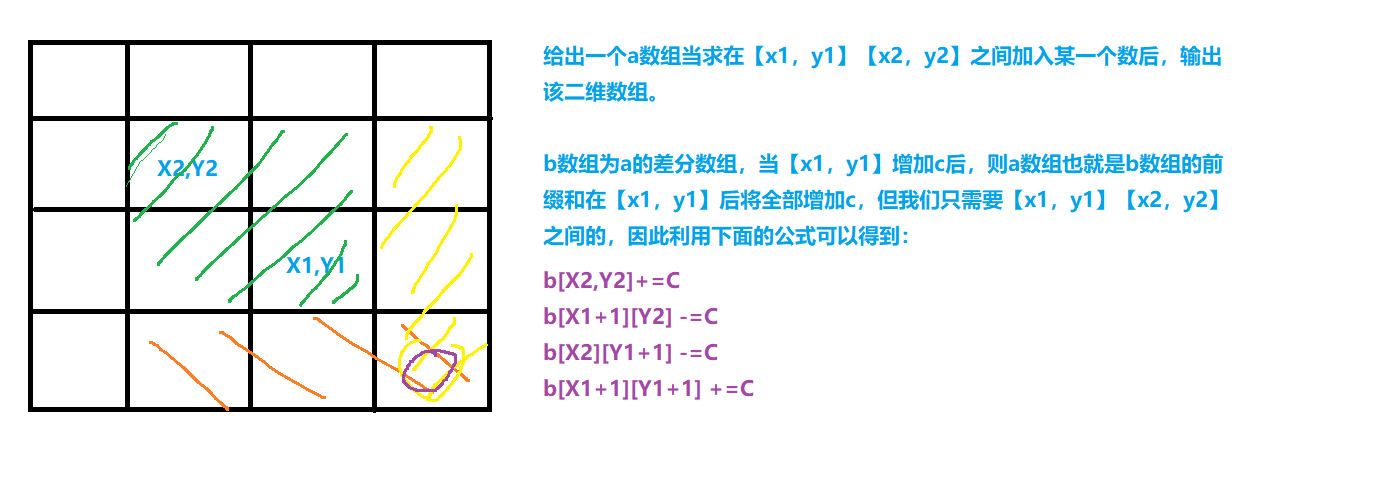
差分（前缀和的逆运算）

一维差分

如果给出数组为b , a数组为b数组的前缀和数组，则b数组称为差分数组，。

差分数组一般运用在，给出一个数组，求数组在[l,r]区间内加上某个数之后的数组是多少的问题：

也就是如果要计算这种问题则，则先构造一个差分数组（b[i] = a[i]-a[i-1]）。

再将他的差分数组按照以下公式计算即可：

B[l] += c, B[r + 1] -= c

因此，如果要在原数组中改变，。则需要O(n)的时间，但使用差分数组，则只需要改变它的差分数组中的两个数即可，时间复杂度为线性的。

image-20220616152317862

例题：

image-20220616152431442

代码为：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
import java.util.*;
public class Main{
    static int N = 100010;
    static int a[] = new int [N];
    static int b[] = new int [N];
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();
        int m  = scanner.nextInt();
        for (int i = 1;i<=n;i++){
            a[i] = scanner.nextInt();
        }
        //求a数组的差分数组--》b 这一步也可以使用insert方法，就是每次像b数组中加入一个小单元格，因为b初始的时候都是0
        for (int i = 1;i<=n;i++){
            b[i] = a[i] - a[i-1];
        }
        while (m-->0){
            int l = scanner.nextInt();
            int r = scanner.nextInt();
            int c = scanner.nextInt();
            insert(l,r,c);
        }
        //求从差分数组的前缀数组，并输出。因为将原数组差分之后还要转换回去才行
        for (int i = 1;i<=n;i++){
            b[i] = b[i-1] + b[i];
        }
        for (int i = 1;i<=n;i++){
            System.out.print(b[i]+" ");
        }
    }
    //增加差分中两个数的方法
    public static void insert(int l,int r,int c){  //使用的就是上面所说的公式
        b[l] = b[l] + c;
        b[r+1] = b[r+1] - c;
    }
}

二维差分

S[i, j] = 第i行j列格子左上部分所有元素的和
以(x2, y2)为左上角，(x1, y1)为右下角的子矩阵的和为：

image-20220616162713636

例题：

image-20220616160111643

代码为：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
import java.util.*;
public class Main{
    static int N = 1010;
    static int M = 1010;
    static int a[][] = new int[N][M];
    static int b[][] = new int[N][M];
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();
        int m = scanner.nextInt();
        int q = scanner.nextInt();
        for (int i = 1;i<=n;i++){
            for (int j = 1;j<=m;j++){
                a[i][j] = scanner.nextInt();
            }
        }
        for (int i = 1;i<=n;i++){
            for (int j = 1;j<=m;j++){
                insert(i,j,i,j,a[i][j]);  //求二维数组的差分数组
            }
        }
        while (q-->0){
            int x1 = scanner.nextInt();
            int y1 = scanner.nextInt();
            int x2 = scanner.nextInt();
            int y2 = scanner.nextInt();
            int c = scanner.nextInt();
            insert(x1,y1,x2,y2,c);
        }

        //求出b的前缀和
        for (int i = 1;i<=n;i++){
            for (int j = 1;j<=m;j++){
                b[i][j] = b[i-1][j] + b[i][j-1] - b[i-1][j-1] + b[i][j];
            }
        }
        //输出
        for (int i = 1;i<=n;i++){
            for (int j = 1;j<=m;j++){
                System.out.print(b[i][j]+" ");
            }
            System.out.println();
        }
    }
    public static void insert(int x1,int y1,int x2,int y2,int c){
        b[x1][y1] +=c;
        b[x2+1][y1] -=c;
        b[x1][y2+1] -=c;
        b[x2+1][y2+1] +=c;
    }
}

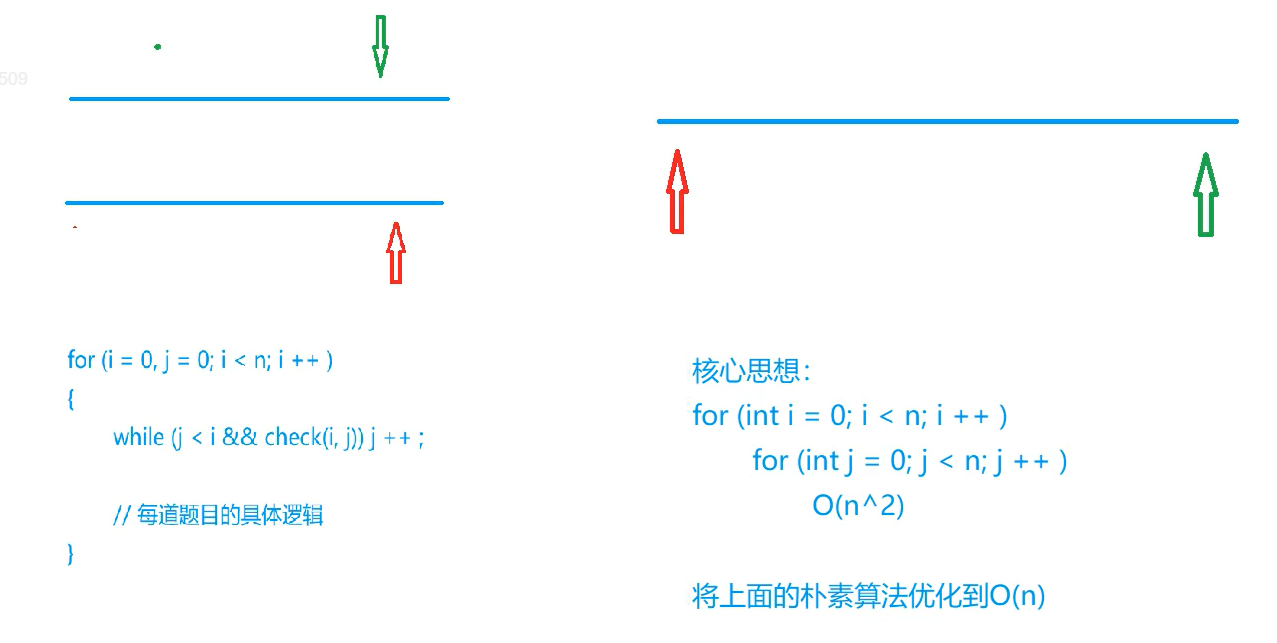
双指针

常见问题分类：
(1) 对于一个序列，用两个指针维护一段区间
(2) 对于两个序列，维护某种次序，比如归并排序中合并两个有序序列的操作

image-20220617085834965

模板：

1
2
3
4
5
6
for (int i = 0, j = 0; i < n; i ++ )
{
    while (j < i && check(i, j)) j ++ ;

    // 具体问题的逻辑
}

例题：

image-20220617100023712

代码1为（使用数组）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
import java.util.*;
public class Main{
    static int N = 100010;
    static int a[] = new int[N];
    static int s[] = new int[N];  //当前区间内，每个i出现的次数
    public static void main(String[] args) {
        Scanner scanner =  new Scanner(System.in);
        int n = scanner.nextInt();
        for (int i = 0;i<n;i++){
            a[i] = scanner.nextInt();
        }
        int res = 0;
        //双指针
        for (int i = 0,j = 0;i<n;i++){
            s[a[i]]++;
            while (j<=i && s[a[i]]>1) {
                s[a[j]]--;
                j++;
            }
            res = Math.max(res,i-j+1);
        }
        System.out.println(res);
    }
}

代码2为（使用哈希表），当判断的元素不是整数的时候，又可能是字母时，要使用哈希表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
import java.util.*;
public class Main{
    static int N = 100010;
    static int a[] = new int[N];
    static Map<Object,Integer> map = new HashMap<>();
    public static void main(String[] args) {
        Scanner scanner =  new Scanner(System.in);
        int n = scanner.nextInt();
        for (int i = 0;i<n;i++){
            a[i] = scanner.nextInt();
        }
        int res = 0;
        //双指针
        for (int i = 0,j = 0;i<n;i++){
            if (map.containsKey(a[i])) map.put(a[i],map.get(a[i])+1);
            else map.put(a[i],1);
            while (j<=i && map.get(a[i])>1) {
                map.put(a[j], map.get(a[j]) - 1);
                j++;
            }
            res = Math.max(res,i-j+1);
        }
        System.out.println(res);
    }
}

位运算

求n二进制中的第k位数字模板：

n >> k & 1

删除二进制中最后一个1

n&n-1

返回二进制中的最后一个 1

n & -n

例题：

image-20220617113253137

代码1为（使用n&(n-1)）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
import java.util.*;
public class Main{
    static int N = 100010;
    static int a[] = new int[N];
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n  =scanner.nextInt();
        for (int i = 0;i<n;i++){
            a[i] = scanner.nextInt();
        }
        for (int i = 0;i<n;i++){
            int res = 0;
            while (a[i]!=0){
                a[i] = a[i]&a[i]-1;
                res++;
            }
            System.out.print(res+ " ");
        }
    }
}

代码2为 （使用n&-n）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
static int N = 100010;
    static int a[] = new int[N];
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n  =scanner.nextInt();
        for (int i = 0;i<n;i++){
            a[i] = scanner.nextInt();
        }
        for (int i = 0;i<n;i++){
            int res = 0;
            while (a[i]!=0){
                a[i] = a[i]-(a[i]&(-a[i]));
                res++;
            }
            System.out.print(res+ " ");
        }
    }

离散化

针对什么样的问题？

当对于所求数的值域非常大，但在实际的操作过程中，却只用到了一部分的数据，比如求 【l，r】之间的和，只用到了【l，r】之间的数，这时又可能想到利用前缀和的方式，进行计算，但是，值域很大 例如在10的-9次幂，到10的9次幂之间，设置一个数组很显然，不现实

因此，要使用离散化进行数据的映射，将用到的数据，映射到新的链表中，

image-20220617222653747

例题：

image-20220617215642689

代码为l;

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
import java.util.*;
public class Main{
    static int N = 300010;
    static List<Integer> alls = new ArrayList<>();//存储操作的下标的询问的下标，也就是需要访问到的下标都要存储进去
    static int a[] = new int[N];
    static int s[] = new int[N];
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();//操作次数
        int m = scanner.nextInt();//询问次数

        List<Pair> pairn = new ArrayList<>();
        List<Pair> pairm = new ArrayList<>();

        for (int i =0;i<n;i++){
            int x = scanner.nextInt();
            int c = scanner.nextInt();
            pairn.add(new Pair(x,c));
            alls.add(x);
        }

        for (int i = 0;i<m;i++){
            int l = scanner.nextInt();
            int r = scanner.nextInt();
            pairm.add(new Pair(l,r));
            alls.add(l);
            alls.add(r);
        }

        //排序
        Collections.sort(alls);
        //和去重
        int p = unique();
        alls = alls.subList(0,p);
        
        for (Pair pn:pairn){
            int i = find(pn.first);
            a[i] = a[i] + pn.second;
        }
        //对a[i]进行求前缀和
        for (int i = 1;i<=alls.size();i++) s[i] = s[i-1]+a[i];
//遍历询问
        for (Pair pm:pairm){
            int l = find(pm.first);
            int r = find(pm.second);
            System.out.println(s[r]-s[l-1]);
        }

    }
    //找到在alls所对应的下标
    public static int find(int x){
        int l = 0;
        int r = alls.size()-1;
        while (l<r){
            int mid = l+r>>1;
            if (alls.get(mid)>=x) r = mid;
            else l = mid + 1;
        }
        return r+1;
    }
//去掉alls中的重复元素
    public static int unique(){
        int j = 0;
        for (int i = 0;i<alls.size();i++){
            if (i==0 || alls.get(i)!=alls.get(i-1)){
                alls.set(j,alls.get(i));
                j++;
            }
        }
        return j;
    }

}
class Pair{
    int first;
    int second;

    public Pair(int first, int second) {
        this.first = first;
        this.second = second;
    }
}

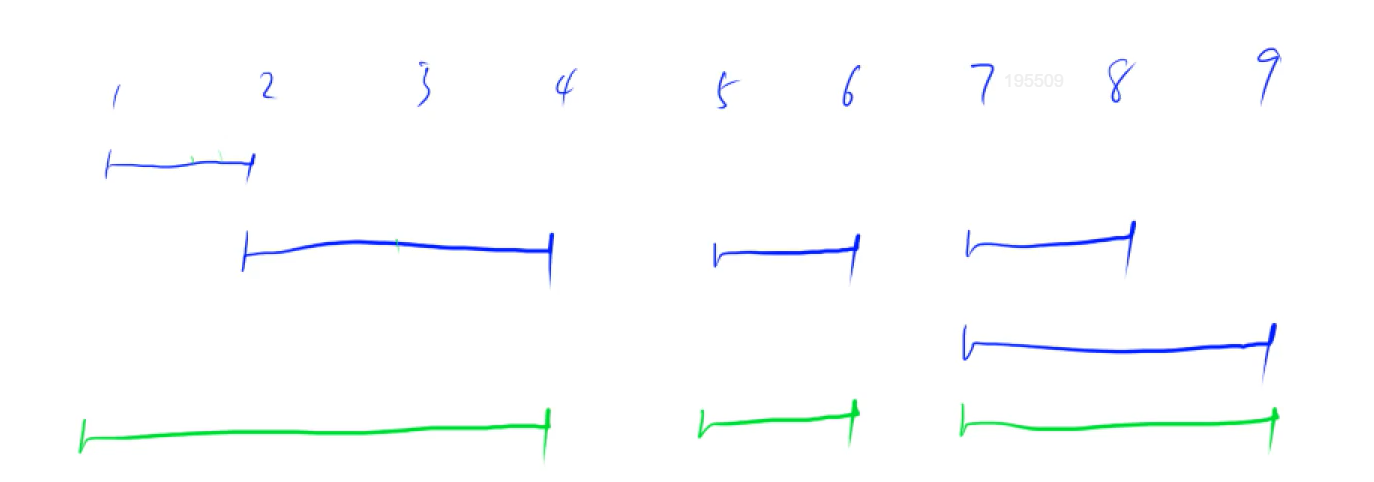
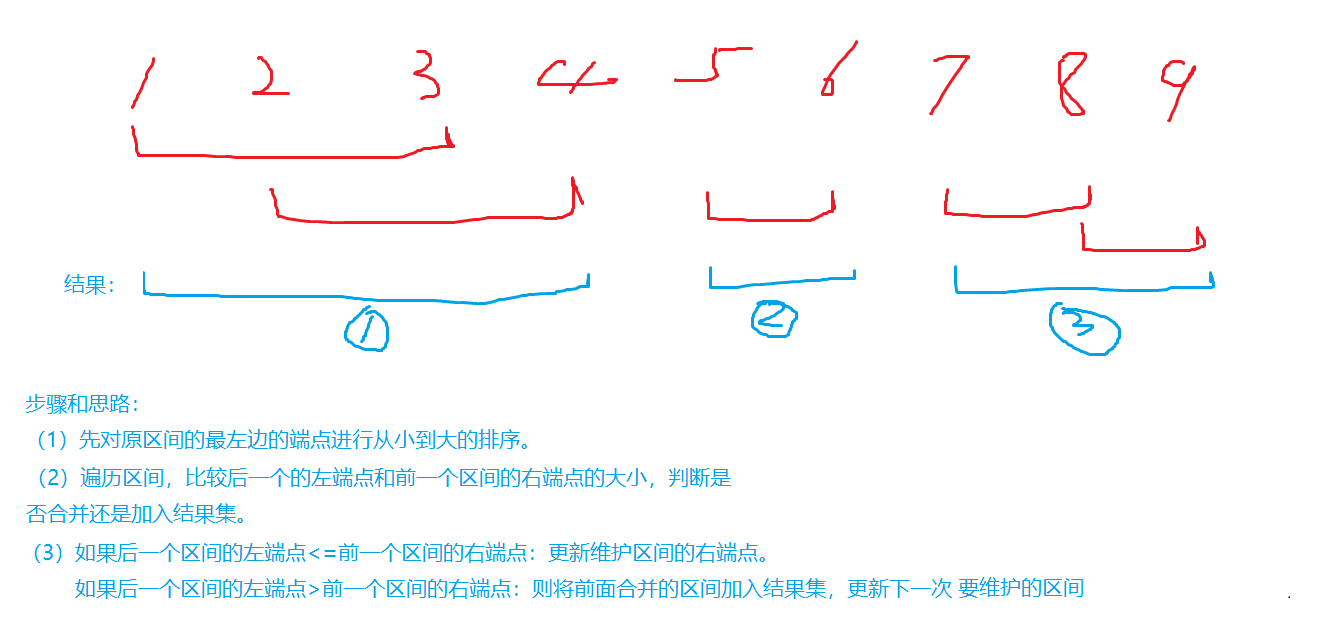
区间合并

题型：

有n个区间，把所有 有交集的区间进行合并，最后求出合并后区间的个数

多个区间，如果有交集的就进行合并。如下图所示：最后合并完的区间为3个

image-20220617223228718

思想和步骤：

image-20220618114041739

代码模板：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int l = (int)(-2*Math.pow(10,9));
int r = (int)(-2*Math.pow(10,9));
for (int k[]:list){
	//新区间的左端点大于前面区间的右端点，说明没有交集，要把之前的那个区间存入到结果集中
	if (k[0]>r){
		//如果不是第一个区间，则加入，之前已经合并之后的区间
		if (l!=(int)(-2*Math.pow(10,9))) res.add(new int[]{l,r});
		//维护下一个区间
		l = k[0];
		r = k[1];
	}
	//有交集的情况，更新最右端点
	r = Math.max(r,k[1]);
}
//将最后一组加入结果集
if (l!=(int)(-2*Math.pow(10,9))) res.add(new int[]{l,r});

例题：

image-20220618114104011

代码为：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
import java.util.*;
public class Main{
    static int N = 100010;
    static int a[];
    static List<int[]> list = new ArrayList<>();
    static List<int[]> res = new ArrayList<>();
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();
        for (int i = 0;i<n;i++){
            a = new int[2];
            int l = scanner.nextInt();
            int r = scanner.nextInt();
            a[0] = l;
            a[1] = r;
            list.add(a);
        }
        list.sort(new Comparator<int[]>() {
            @Override
            public int compare(int[] o1, int[] o2) {
                return o1[0]-o2[0];
            }
        });
        int l = (int)(-2*Math.pow(10,9));
        int r = (int)(-2*Math.pow(10,9));
        //区间合并模板
        for (int k[]:list){
            //新区间的左端点大于前面区间的右端点，说明没有交集，要把之前的那个区间存入到结果集中
            if (k[0]>r){
                if (l!=(int)(-2*Math.pow(10,9))) res.add(new int[]{l,r});
                //维护下一个区间
                l = k[0];
                r = k[1];
            }
            //有交集，更新最右端点。
            r = Math.max(r,k[1]);
        }
        //将最后一组加入结果集
        res.add(new int[]{l,r});
        System.out.println(res.size());
    }
}
算法 > 模板
#算法
模板1-基础算法
http://example.com/2022/06/15/模板/
作者
zlw
发布于
2022年6月15日
许可协议