汉明距离

leetCode–461（汉明距离）

两个整数之间的 汉明距离 指的是这两个数字对应二进制位不同的位置的数目。

给你两个整数 x 和 y，计算并返回它们之间的汉明距离。

示例 1：

输入：x = 1, y = 4
输出：2
解释：
1   (0 0 0 1)
4   (0 1 0 0)
       ↑   ↑
上面的箭头指出了对应二进制位不同的位置。

示例 2：

输入：x = 3, y = 1
输出：1

解法一：内置函数

汉明距离：就是两个二进制位中不同位置的数目。

两个整数二进制位中不同的数目：就是两个数进行异或 ， 结果为 1 的数目。

首先可以使用java中的内置方法，。Integer.bitCount()，用来求二进制中为1 的数目。

代码为：

class Solution {
    public int hammingDistance(int x, int y) {
        //异或后求1的个数就是二进制中不同位置的个数，也就是汉明距离
        return Integer.bitCount(x^y);
    }
}

解法二：移位实现位计数

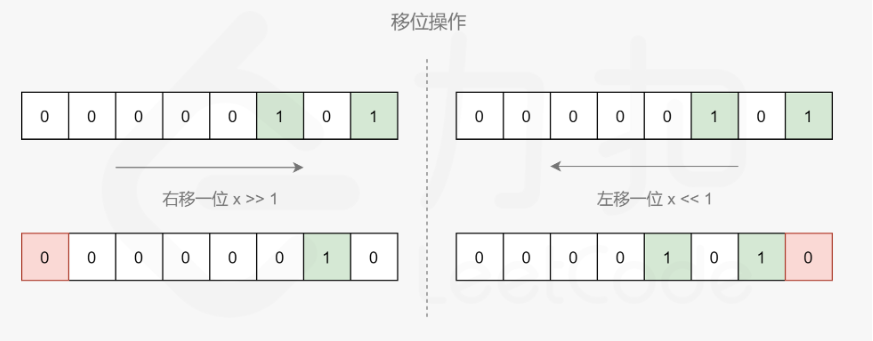
我们可以不断地检查 s 的最低位，如果最低位为 1，那么令计数器加一，然后我们令 s 整体右移一位，这样 s 的最低位将被舍去，原本的次低位就变成了新的最低位。我们重复这个过程直到 s=0 为止。这样计数器中就累计了 s 的二进制表示中 1 的数量。

代码为：

class Solution {
    public int hammingDistance(int x, int y) {
        //异或，通过移位的方法计算1 的个数
        //每次像右移动一位。如果最低位为1，则数量加1
        int a = x^y;
        int count = 0;
        while (a!=0){
            //判断最低为是否为1 
            if ((a&1)==1) count++;
            a = a>>1;
        }
        return count;
    }
}

解法三：Brian Kernighan 算法

在解法二的位移动方法中，对于 s=(10001100)的情况，我们需要循环右移 8 次才能得到答案。而实际上如果我们可以跳过两个 11 之间的 00，直接对 11 进行计数，那么就只需要循环 33 次即可。

可以使用 Brian Kernighan 算法进行优化。

Brian Kernighan 算法： 当进行x&(x-1)时，时删除x二进制位中最右侧的 1 。

这样就大大减少了，对0 的移动次数

代码为：

class Solution {
    public int hammingDistance(int x, int y) {
        //异或 通过使用Brian Kernighan 算法，对移位算法进行优化
        //因为移位要每次移动一位，但Brian Kernighan 算法时删除最后一个1，每次移动多位，直到遇到0
        int a = x^y;
        int count = 0;
        while (a!=0){
            a = a&(a-1);
            count++;
        }
        return count;
    }
}