十大排序算法

冒泡排序

两两进行比较，进行一遍遍历就将最大的数放到最右端。放在最右端的数在下一次遍历中不用遍历，因为已经是有序的。
代码为：

/**
     * 冒泡排序
     * @param arr
     */
public void bubbleSort(int arr[]){
    int n = arr.length;
    for (int i = 0;i<n;i++){
        for (int j = 0;j<n-1-i;j++){
            if (arr[j]>arr[j+1]){
                int t = arr[j];
                arr[j] = arr[j+1];
                arr[j+1] = t;
            }
        }
    }
}

也可以进行一下简单的优化：

/**
     * 冒泡排序的优化
     * @param arr
     */
public void bubbleSort(int arr[]){
    int n = arr.length;
    boolean f = false;
    for (int i = 0;i<n;i++){
        f = false;
        for (int j = 0;j<n-1-i;j++){
            if (arr[j]>arr[j+1]){
                int t = arr[j];
                arr[j] = arr[j+1];
                arr[j+1] = t;
                f = true;
            }
        }
        if (f== false) break;
    }
}

插入排序

将第一个元素看作有序序列，从数组的第二个位置进行扫描，依次与它之前的数字进行比较，如果遍历到的数字小于前面已经遍历过的数，则前面的数依次后移，直到找到不大于该数的位置，停止本次的遍历，讲该数放入得到这个位置中。

代码为：

/*
插入排序
 */
public void insertSort(int arr[]){
    int n = arr.length;
    for (int i = 1;i<n;i++){
        int j = i;
        int t = arr[j];
        if (t<arr[j-1]){
            while (j-1>=0 && t<arr[j-1]){
                arr[j] = arr[j-1];
                j--;
            }
        }
        arr[j] = t;
    }
}

选择排序

如果是从小到大的排序，从序列中找到最小元素放入开头，再从剩下的序列中找到最小元素，依次放入之后，依次进行。

代码为：

/**
 * 选择排序
 * @param arr
 */
public void selectSort(int arr[]){
    int n = arr.length;
    int min;
    int t = 0;
    for (int j = 0;j<n;j++) {
        min = arr[j];
        t = j;
        for (int i = j+1; i < n; i++) {
            if (arr[i] < min) {
                min = arr[i];
                t = i;
            }
        }
        if (t!=j){
            int m = arr[j];
            arr[j] = arr[t];
            arr[t] = m;
        }
    }
}

希尔排序

与插入排序类似，插入排序是每次与它前一个元素进行比较，而希尔排序是每次进行几跳的元素比较。

/**
     * 希尔排序
     * @param arr
     */
    public void shellSort(int arr[]){
        int n = arr.length;
        for (int gap = n/2;gap>0;gap = gap/2){
            for (int i = gap;i<n;i++){
                int j = i;
                int t = arr[i];
                if (arr[j-gap]>t){
                    while (j-gap>=0 && arr[j-gap]>t){
                        arr[j] = arr[j-gap];
                        j = j-gap;
                    }
                }
                arr[j] = t;
            }
        }
    }

快速排序

找到一个基准值，每次将比基准值小的数放在基准值的左边，比基准值大的数放在基准值的右边。
代码为：

/**
     * 快速排序
     * @param arr
     * @param l
     * @param r
     */
    public void quickSort(int arr[],int l,int r){
        if (l<r){
            int index = sort(arr,l,r);
            quickSort(arr,l,index-1);
            quickSort(arr,index+1,r);
        }
    }
    public int sort(int arr[],int l,int r){
        int t = arr[l];
        while (l<r){
            while (l<r && arr[r]>=t){
                r--;
            }
            if (arr[r]<t){
                arr[l] = arr[r];
            }
            while (l<r && arr[l]<=t){
                l++;
            }
            if (arr[l]>t){
                arr[r] = arr[l];
            }
        }
        arr[l] = t;
        return l;
    }

归并排序

解法一：递归写法

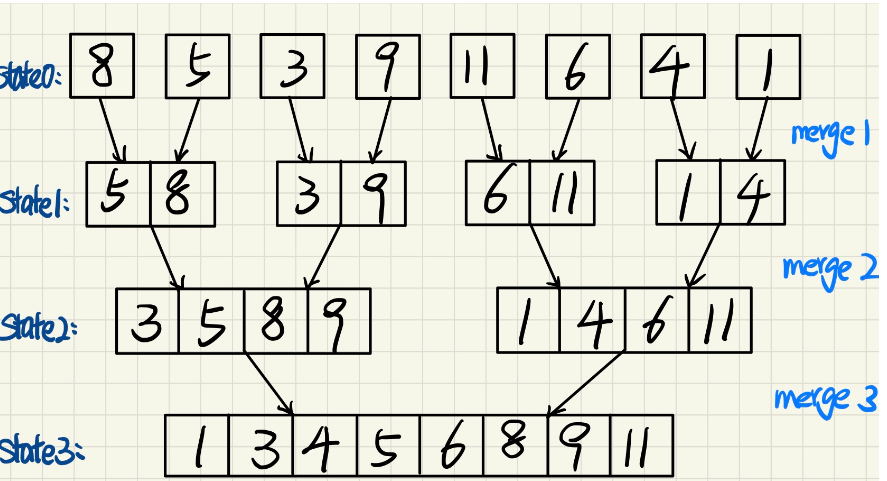
把一组n个数的序列，折半分为两个序列，然后再将这两个序列再分，一直分下去，直到分为n个长度为1的序列。然后两两按大小归并。如此反复，直到最后形成包含n个数的一个数组。

代码为：

/*
归并排序，递归写法
 */
public void mergeSort(int arr[],int l,int r){
    if (l<r){
        int mid = (l+r)/2;
        mergeSort(arr,l,mid);
        mergeSort(arr,mid+1,r);
        merge(arr,l,r,mid);
    }
}
public void merge(int arr[],int l,int r,int mid){
    int i = l;
    int j = mid+1;
    int temp[] = new int[arr.length];
    int index = 0;
    while (i<=mid && j<=r){
        if (arr[i]<arr[j]){
            temp[index++] = arr[i];
            i++;
        }else {
            temp[index++] = arr[j];
            j++;
        }
    }
    while (i<=mid){
        temp[index++] = arr[i++];
    }
    while (j<=r){
        temp[index++] = arr[j++];
    }
    //临时数组复制到原数组
    for (int a = 0;a<index;a++){
        arr[l++] = temp[a];
    }
}

解法二：非递归解法

/**
    * 归并排序，非递归写法
    * 递归方法的归并是，将原始数组一点一点缩小，而非递归相当于二叉树，从数的叶子节点开始合并
    * 合并时，数组的个数为1，2，4，8，。。。
    */
   public void mergeSort(int arr[]){
       int n = arr.length;
       int l,mid,r;
       for (int i = 1;i<n;i = i+i){
           l = 0;
           mid = l+i-1;
           r = mid+i;
           while (r<n){
               //合并数组
               merge(arr,l,r,mid);
               l = r+1;
               mid = l+i-1;
               r = mid+i;
           }
           //还有一些被遗漏的数组没合并，因为不可能每个数组的大小都刚好为i
           if (l<n && mid<n){
               merge(arr,l,n-1,mid);
           }
       }
   }
   public void merge(int arr[],int l,int r,int mid){
       int i = l;
       int j = mid+1;
       int temp[] = new int[arr.length];
       int index = 0;
       while (i<=mid && j<=r){
           if (arr[i]<arr[j]){
               temp[index++] = arr[i];
               i++;
           }else {
               temp[index++] = arr[j];
               j++;
           }
       }
       while (i<=mid){
           temp[index++] = arr[i++];
       }
       while (j<=r){
           temp[index++] = arr[j++];
       }
       //临时数组复制到原数组
       for (int a = 0;a<index;a++){
           arr[l++] = temp[a];
       }
   }

归并排序的时间复杂度的计算

归并排序的总时间复杂度 = 分解时间 + 子序列排序的时间 + 合并时间

因为每次都是从数组的中间分解所以，分解的时间复杂度为常数，可以忽略。

因此 归并排序的时间复杂度 = 子序列排序的时间 + 合并时间

那么我们将n个数的序列，分为两个(n/2)的序列。

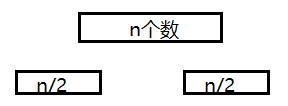
因为合并时组内已经排序完成，所以时间复杂度为n，那么T(n)=2*T(n/2)+n

我们再将两个n/2个序列再分成4个(n/4)的序列。

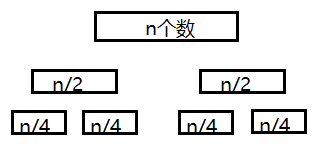
一个（n/2）序列排序时间 = 两个(n/4)的序列排序时间 + 两个(n/4)的序列的合并为一个（n/2）的序列时间

T(n/2)=2*T(n/4)+n/2

将T(n/2)带入到T(n)中，T(n)=2*(2*T(n/4)+n/2)+n，

通过化简T(n)=4*T(n/4)+2n

依次计算为：

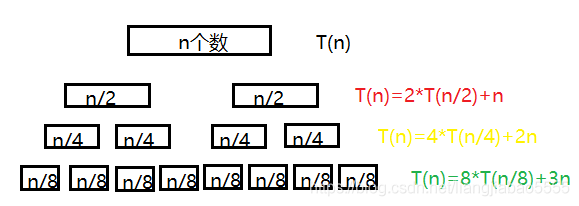
这个图就像二叉树一样，我们知道，一个n个结点的二叉树层数为(log2n)+1

根据这个图的n前面的系数可以得出，n前面的系数为层数-1。(log2n)+1-1=log2n

因此log2n就是最底层n的系数。

那么我们最后一层是不是可以这样表示

T(n)=n*T(1)+(log2n)*n

T(1)=0，那么T(n)=(log2n)*n

所以归并排序的时间复杂度为nlog2n

基数排序

每次遍历依次将元素放入到10个桶中，0–9，进行遍历的次数由最大值的位数决定，

基数排序的思想是先以个位数的大小进行排序，再以十位数大小进行排序。。。。

代码为：

/**
 * 基数排序
 * @param arr
 */
public void radixSort(int arr[]){
    int n = arr.length;
    int max = arr[0];
    for (int i = 1;i<n;i++){
        if (max<arr[i]){
            max = arr[i];
        }
    }
    int len = (max+"").length();
    int bucket[][] = new int[10][n];
    int bucketSize[] = new int[10];
    for (int l = 0,gap = 1;l<len;gap = gap*10,l++){
        for (int i = 0;i<n;i++){
            int a = arr[i] / gap % 10;
            bucket[a][bucketSize[a]] = arr[i];
            bucketSize[a]++;
        }
        int index = 0;
        //遍历桶中的元素加入到arr中
        for (int i = 0;i<10;i++){
            if (bucketSize[i]!=0){
                for (int j = 0;j<bucketSize[i];j++){
                    arr[index++] = bucket[i][j];
                }
            }
            bucketSize[i] = 0;
        }
    }
}

堆排序

先将数组变成大顶堆的数组，之后将第一个元素和最后一个元素进行交换，再对前n-1个元素进行循环大顶堆的操作，每次循环都将第一个元素与n-i个位置的元素进行交换。

代码为：

/**
 * 堆排序
 * @param arr
 */
public void heapSort(int arr[]){
    //最后一个非叶子节点开始进行大顶堆的操作，最后一个非叶子节点为：arr.length/2-1
    for (int i = arr.length/2-1;i>=0;i--){
        bigHeap(arr,i,arr.length);
    }
    for (int i = arr.length-1;i>=0;i--){
         //将第一个元素与最后一个元素进行交换，也就是把最大的元素放到数组的最后
        if (arr[0]>arr[i]){
            int t = arr[0];
            arr[0] = arr[i];
            arr[i] = t;
        }
         //将最后一个元素剩下的，前面的元素进行大顶堆的操作
        bigHeap(arr,0,i);
    }
}
//大顶堆
public static void bigHeap(int arr[],int i,int n){
    int t = arr[i];
     //节点的左子树：i*2+1
    for (int a = 2*i+1;a<n;a = a*2+1){
         //判断左子树和右子树节点哪个大，选择大的哪个
        if (a+1<n && arr[a]<arr[a+1]){
            a++;
        }
        //如果当前节点没有左子树或者右子树中最大的节点大
        if (arr[i]<arr[a]){
            arr[i] = arr[a];//将左子树和右子树中大的节点与它的根节点（也就是当前的节点进行交换）
            i = a;//接着将节点赋予左右子树中大的节点继续后面的操作，为了判断它下面是否还有子树
        }else break;
        arr[a] = t;
    }
}

方法二：

public class heap {
    static int N = 100010;
    static int h[] = new int[N];
    static int size;
    public static void down(int a){
        int u = a;
        if (2*a<=size && h[u]>h[2*a]) u = 2*a;
        if (2*a+1<=size && h[u]>h[2*a+1]) u = 2*a+1;
        if (u!=a){
            swap(u,a);
            down(u);
        }
    }
    public static void swap(int x,int y){
        int temp = h[x];
        h[x] = h[y];
        h[y] = temp;
    }

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n  = scanner.nextInt();
        int m = scanner.nextInt();
        for (int i = 1;i<=n;i++){
            h[i] = scanner.nextInt();
        }
        size = n;
        //构造一个堆
        for (int i = n/2;i>=0;i--){
            down(i);
        }
        while (m-->0){
            System.out.print(h[1]+" ");
            h[1] = h[size];
            size--;
            down(1);
        }
    }
}

计数排序

元素的大小对应数组的下标。
新建数组将遍历原数组元素，将原数组的元素存放对应的新建数组下标中。新建数组表示：temp[5] = 2：5这个数有2个。
最后依次遍历新建数组放入原数组中。

代码为：

/**
 * 计数排序，普通方法
 * @param arr
 */
public void countSort(int arr[]){
    int n = arr.length;
    int max = arr[0];
    for (int i = 1;i<n;i++){
        if (max<arr[i]){
            max = arr[i];
        }
    }
    int bucket[] = new int[max+1];
    for (int i = 0;i<n;i++){
        bucket[arr[i]]++;
    }
    int index = 0;
    for (int j = 0;j<=max;j++){
        if (bucket[j]!=0){
            for (int a = 0;a<bucket[j];a++){
                arr[index++] = j;
            }
        }
    }
}

优化后的代码：

优化一：当使用普通方法进行计数排序时，浪费了很多资源，例如，排序300-900之间的元素，而要建立大小为900的数组，其中前300没有数字，所以浪费了300个数组位置，最好的办法就是只定义300-900之间的这些长度的数组，所以不仅要求出最大值还要求出最小值来定义。

优化二：还有一个问题就是对于普通数进行排序时是可以的，但是在真实的场景中，值相等的数并不能区分谁在前谁在后，对于这个问题，我们在新建的数组上加入偏移量，偏移量等于前面元素的个数+数组的数（这个值表示了排序后数组的位置）

/**
 * 优化的计数排序，主要用于这种情况：
 * 当要排序的数在200-300之内时如果没有优化之前  新建数组的长度为300 但是前200个空间浪费
 * 数组的长度只需要100即可，所以算出最小值，数组的大小在最小值和最大值之间.
 * 还有一个问题就是对于普通数进行排序时是可以的，但是在真实的场景中，值相等的数并不能区分谁在前谁在后
 * 对于这个问题，我们在新建的数组上加入偏移量，偏移量等于前面元素的个数+数组的数（这个值表示了排序后数组的位置）
 */
public int[] countSortGood(int arr[]){
    int n = arr.length;
    int max = arr[0];
    int min = arr[0];
    for (int i = 1;i<n;i++){
        if (max<arr[i]){
            max = arr[i];
        }
        if (min>arr[i]){
            min = arr[i];
        }
    }
    int bucket[] = new int[max-min+1];
    for (int i = 0;i<n;i++){
        bucket[arr[i]-min]++;
    }
    //向后叠加，后面元素等于前面元素之和，。里面的值就是排序后数组的位置
    for (int j = 1;j<bucket.length;j++){
        bucket[j] = bucket[j-1] + bucket[j];
    }
    int sort[] = new int[n];
    //逆序遍历原数组，从统计数组中找到正确的位置，放到结果数组中
    //用例子模拟一遍就知道了
    for (int i = n-1;i>=0;i--){
        if (bucket[arr[i]-min]!=0){
            //因为temp[arr[i]-min]代表位置，sort里面存放是下标，所以减 1
            sort[bucket[arr[i]-min]-1] = arr[i];
            bucket[arr[i]-min]--;
        }
    }
    return sort;
}

桶排序

与计数排序和基数排序都是同等类型，但是它处理的问题更加广泛，可以处理非整数数字的排序。

/**
 * 桶排序
 * @param arr
 */
public void bucketSort(int arr[]){
    int n = arr.length;
    int max = arr[0];
    int min = arr[0];
    for (int i = 1;i<n;i++){
        if (max<arr[i]){
            max = arr[i];
        }
        if (min>arr[i]){
            min = arr[i];
        }
    }
    //计算桶的数量
    int range = (max-min+1)/n;
    List<List<Integer>> list = new LinkedList<>();
    for (int i = 0;i<range;i++){
        list.add(new LinkedList<>());
    }
    //将每个元素放入桶中
    for (int i = 0;i<n;i++){
        int l = (arr[i]-min+1)/range;
        list.get(l).add(arr[i]);
    }
    //对每个桶进行排序
    for (int i = 0;i<range;i++){
        Collections.sort(list.get(i));
    }
    // 将桶中的元素赋值到原序列
    int index = 0;
    for (int i = 0;i<range;i++){
        if (list.get(i)!=null) {
            for (int j = 0; j < list.get(i).size(); j++) {
                arr[index++] = list.get(i).get(j);
            }
        }
    }
}

适用场景

冒泡：适用的情景为数据量量不大，对稳定性有要求，且数据基本有序的情况下

选择：当数据量不大，且对稳定性没有要求的时候，适用于选择排序

插入：如果大部分数据距离它正确的位置很近或者近乎有序？例如银行的业务完成的时间。如果是这样的话，插入排序是更好的选择。

快速：由于快速排序的原理，常用于查找一组中前k大的数据
堆：堆排序适合于数据量非常大的场合（百万数据）。（堆排序会将所有的数据建成一个堆，最大的数据在堆顶，然后将堆顶数据和序列的最后一个数据交换。接下来再次重建堆，交换数据，依次下去，就可以排序所有的数据。）

希尔：当数据量较小的时候适用

计数：计数排序需要占用大量空间，它仅适用于数据比较集中的情况。比如 [0100]，[1000019999] 这样的数据。

桶排序：桶排序(Bucket Sort)对要排序的数据要求较多。
1 要排序的数据需要很容易就能划分成 N 个桶，并且，桶与桶之间有着天然的大小顺序
2 数据在各个桶之间的分布最好比较均匀。否则可能出现，有些桶里的数据非常多，有些非常少，极端情况可能会被 划分到同一个桶中

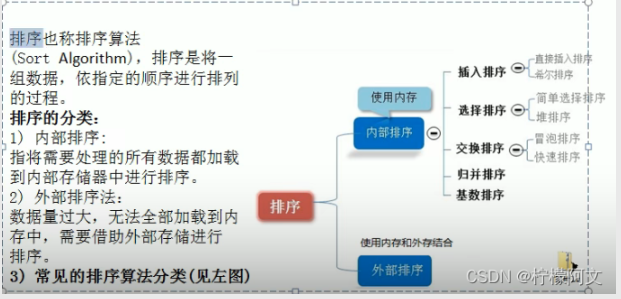
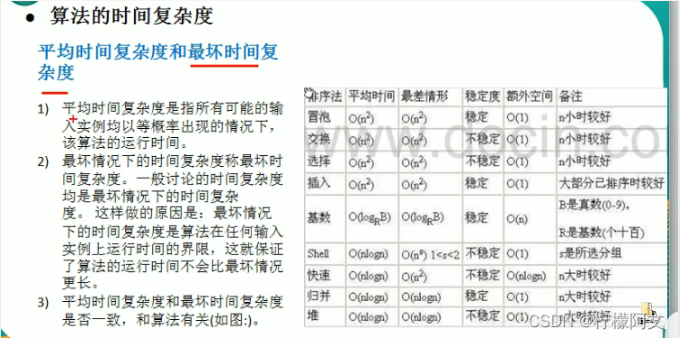
排序算法的分类和复杂度