二叉树的中序遍历
根据leetCode中94题的二叉树中序遍历而整理
给定一个二叉树的根节点 root ,返回 它的 中序 遍历 。
示例 1:
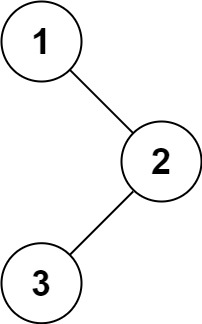
1
2
| 输入:root = [1,null,2,3]
输出:[1,3,2]
|
示例 2:
解法一:递归
最简单的方法,也是很好想到的解法,一开始只会这个 ,哈哈哈。。但总是在进步嘛
中序遍历的访问顺序是:左子树—->根节点—->右子树(在代码中就是左 - 打印 - 右)
由于 访问左子树或者右子树的时候我们按照同样的方式遍历,直到遍历完整棵树。所以具有递归的性质,可以直接用递归函数来模拟这一过程。
递归函数实现:
- 终止条件:当前节点为空时
- 函数内:递归的调用左节点,打印当前节点,再递归调用右节点。
代码为:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
class Solution {
List<Integer> list = new LinkedList<>();
public List<Integer> inorderTraversal(TreeNode root) {
if(root!=null){
if (root.left!=null) inorderTraversal(root.left);
list.add(root.val);
if (root.right!=null) inorderTraversal(root.right);
}
return list;
}
}
|
解法二:迭代
一开是不会这个方法,但是看了官方题解中的动图步骤,竟然自己写出来了!~~加鸡腿!!哈哈
觉得官方题解的步骤太好了,清晰明了,在这里显示一下吧,以免过后忘记了~~记性太差了!!
在递归的过程中,操作系统/虚拟机自动帮我们用栈来保存,所以在迭代的过程中需要自己手动维护一个栈进行实现。
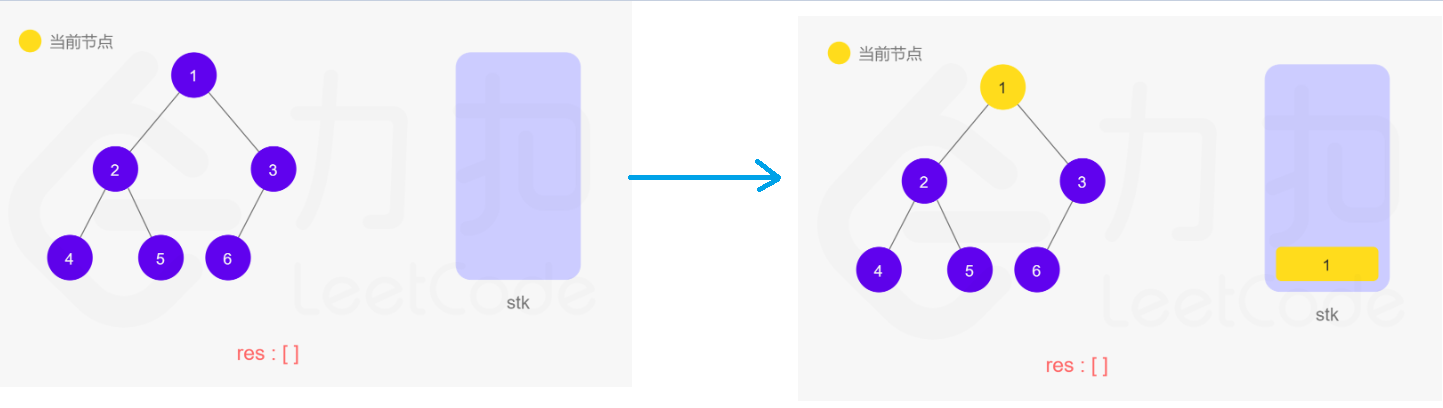
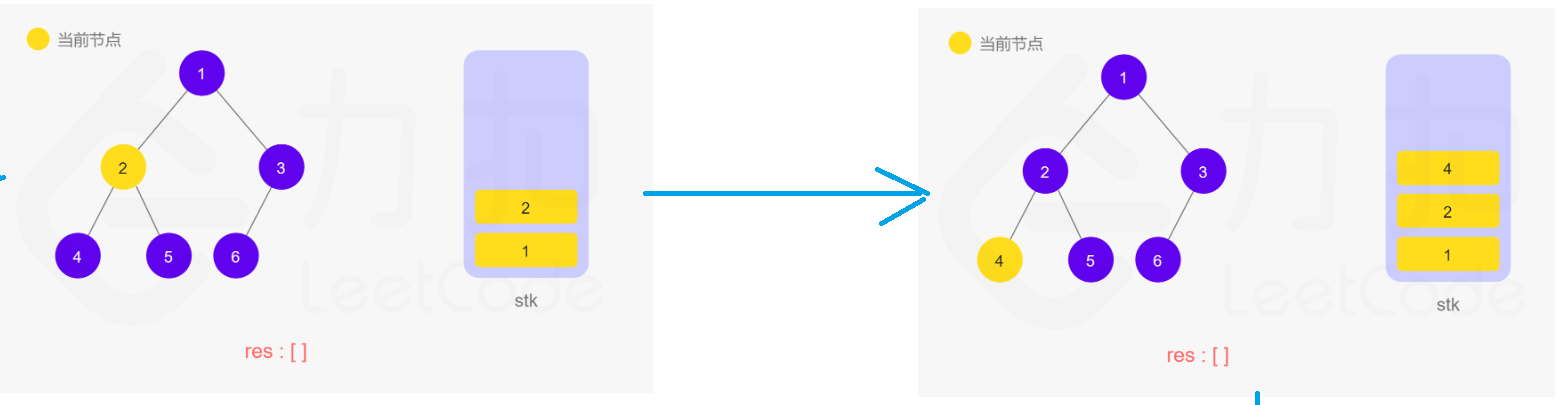
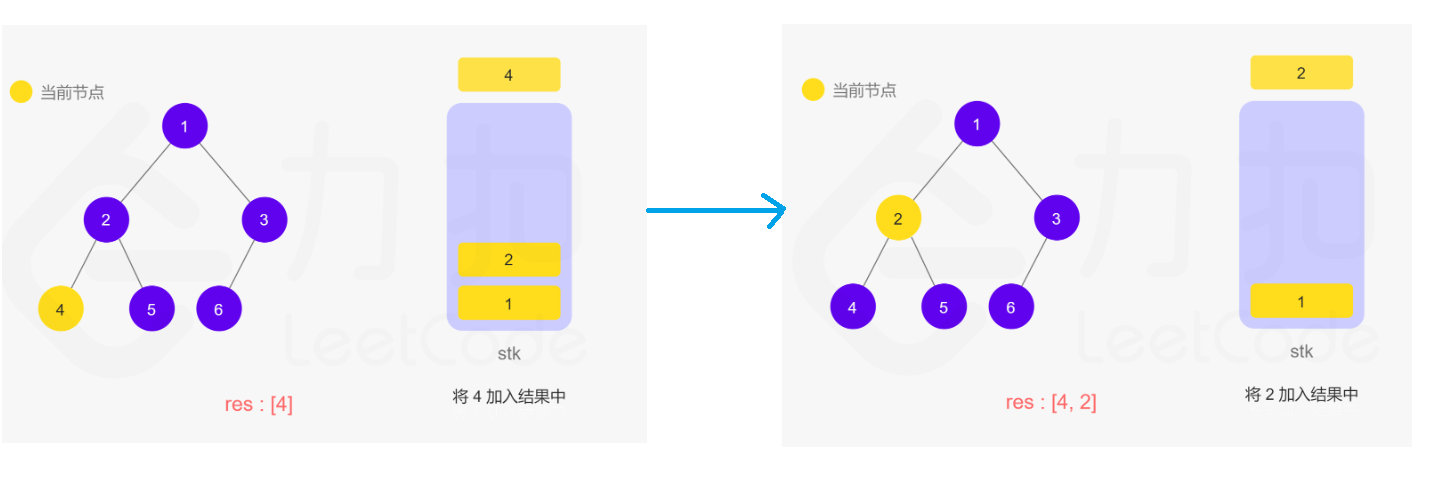
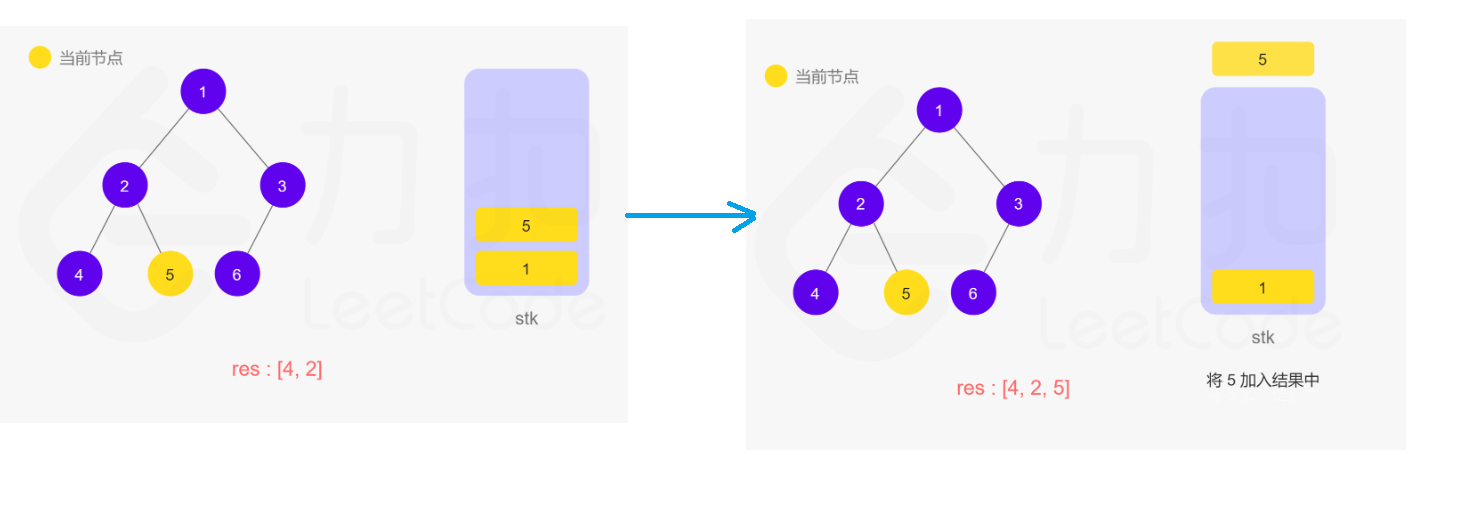
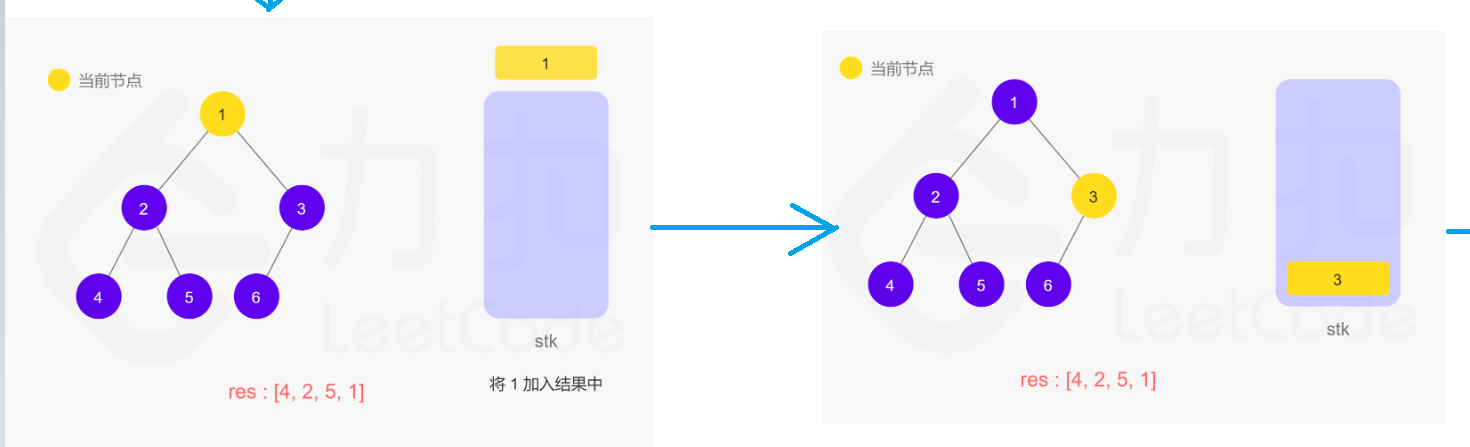
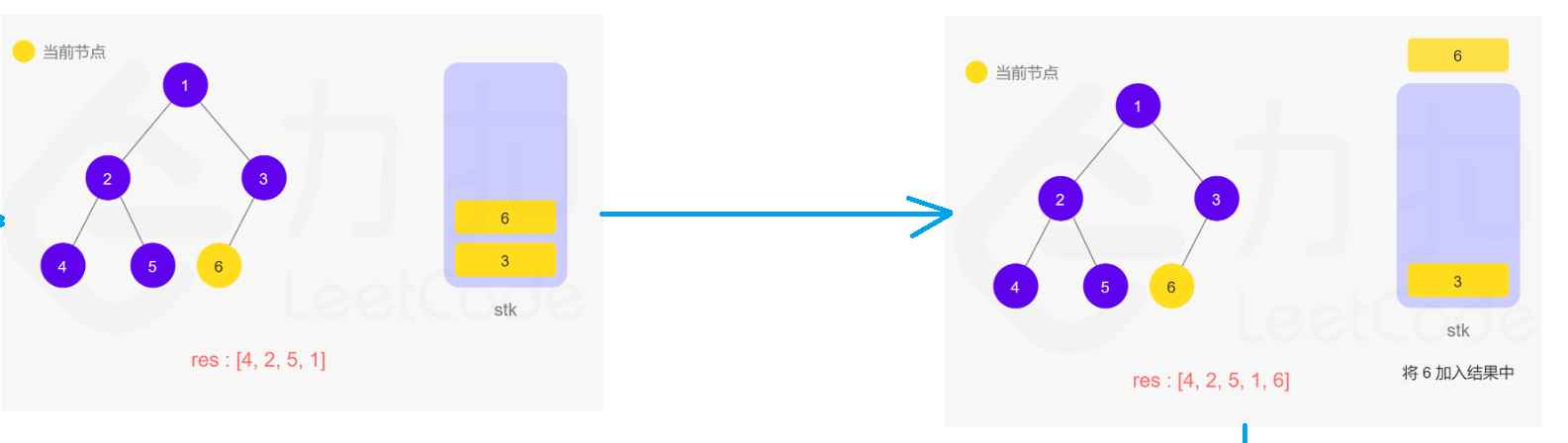
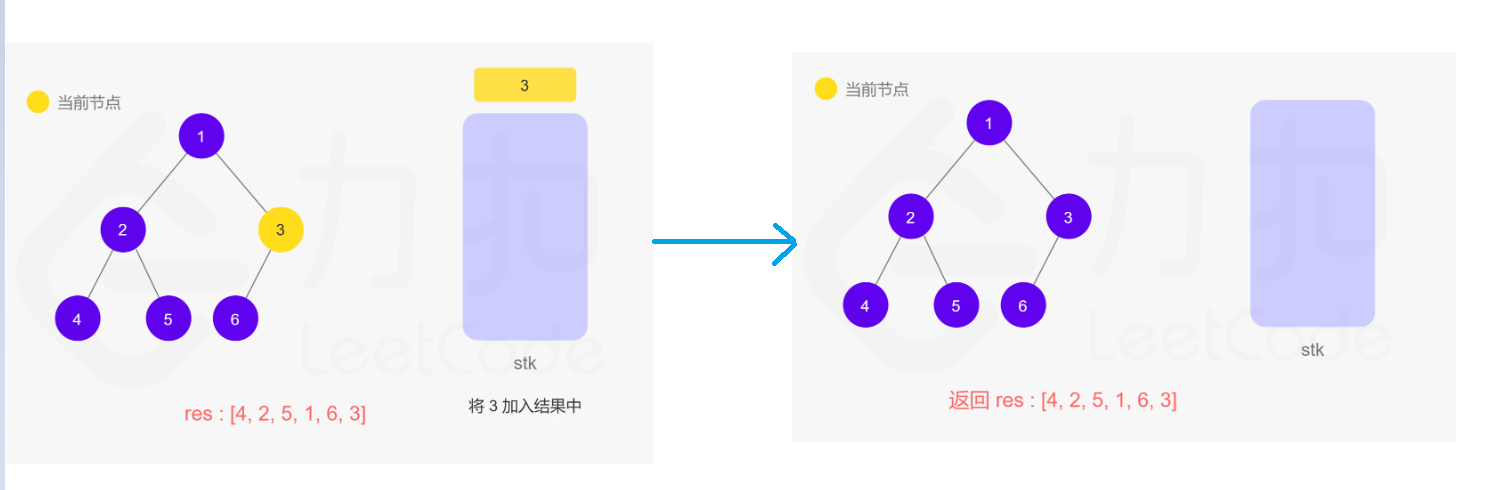
代码为:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<Integer>();
Deque<TreeNode> stk = new LinkedList<TreeNode>();
while (root != null || !stk.isEmpty()) {
while (root != null) {
stk.push(root);
root = root.left;
}
root = stk.pop();
res.add(root.val);
root = root.right;
}
return res;
}
}
|
解法三:Morris
这个算法,由于不需要维护一个栈,所以空间复杂度为O(1)。优点是节省了空间,缺点是改变了整个树的结构,强行把一棵二叉树改成一段链表结构。
Morris 遍历算法整体步骤如下(假设当前遍历到的节点为 x):
(1)如果x没有左孩子,则加入答案组,再访问x的右节点,即:x=x.rigth
(2)如果x有左孩子,则找到x左子树上最右的节点(即左子树中序遍历的最后一个节点,x在中序遍历中的前驱节点),我们记作 predecdssor。根据predecdssor的右孩子是否为空,进行如下操作。
- 如果
predecdssor的右孩子为空,则将其右孩子指向x,然后访问x的左孩子,即x=x.left。
- 如果
predecdssor的右孩子不为空,则此时右孩子指向x,说明我们已经遍历完x的左子树,我们将predecdssor的右孩子置空,将 x 的值加入答案数组,然后访问 x 的右孩子,即 x=x.right。
其实整个过程我们就多做一步:假设当前遍历到的节点为 x,将 x 的左子树中最右边的节点的右孩子指向 x,这样在左子树遍历完成后我们通过这个指向走回了 x,且能通过这个指向知晓我们已经遍历完成了左子树,而不用再通过栈来维护,省去了栈的空间复杂度。
代码为:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
|
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> list = new LinkedList<>();
while (root!=null){
if (root.left!=null) {
TreeNode pre = root.left;
while (pre.right!=null && pre.right!=root){
pre = pre.right;
}
if (pre.right!=null){
list.add(root.val);
root = root.right;
pre.right = null;
}else {
pre.right = root;
root = root.left;
}
}else {
list.add(root.val);
root = root.right;
}
}
return list;
}
}
|
二叉树的前序遍历
leetCode144题
给你二叉树的根节点 root ,返回它节点值的 前序 遍历。
示例 1:

示例 2:
解法一:递归
前序遍历的访问顺序是:根节点—->左子树—->右子树(在代码中就是打印 - 左 - 右)
代码为:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
class Solution {
List<Integer> list = new LinkedList<>();
public List<Integer> preorderTraversal(TreeNode root){
if (root!=null){
list.add(root.val);
if (root.left!=null) preorderTraversal(root.left);
if (root.right!=null) preorderTraversal(root.right);
}
return list;
}
}
|
解法二:迭代
前序遍历的迭代,就是先加入list。
代码为:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
class Solution {
public List<Integer> preorderTraversal(TreeNode root){
List<Integer> list = new LinkedList<>();
Stack<TreeNode> stack = new Stack<>();
while (root!=null || !stack.isEmpty()){
while (root!=null){
list.add(root.val);
stack.add(root);
root = root.left;
}
root = stack.pop();
root = root.right;
}
return list;
}
}
|
解法三:Morris
哇塞今天是很开心的一天呀有着中序遍历中Morris方法的经验,看着下图就爽了,希望不要忘记把,咋可能呢,明天估计就不会了。
代码为:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
|
class Solution {
public List<Integer> preorderTraversal(TreeNode root){
List<Integer> list = new LinkedList<>();
if (root == null) {
return res;
}
TreeNode pre = new TreeNode();
while (root!=null){
list.add(root.val);
if (root.left!=null){
pre = root.left;
while (pre.right!=null && pre.right!=root.right){
pre = pre.right;
}
if (pre.right==null) {
pre.right = root.right;
}else {
pre = pre.right;
list.add(pre.val);
}
root = root.left;
}else {
root = root.right;
}
}
return list;
}
}
|
二叉树的后序遍历
leetCode145题:
给你一棵二叉树的根节点 root ,返回其节点值的 后序遍历 。
示例 1:
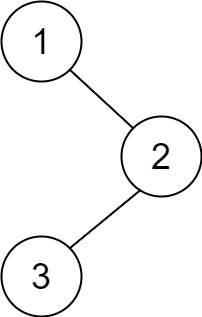
示例 2:
解法一:递归
后序遍历的访问顺序是:左子树—->右子树—->根节点(在代码中就是左 - 右 - 打印)
代码为:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
class Solution {
List<Integer> list = new LinkedList<>();
public List<Integer> postorderTraversal(TreeNode root) {
if (root!=null){
if (root.left!=null) postorderTraversal(root.left);
if (root.right!=null) postorderTraversal(root.right);
list.add(root.val);
}
return list;
}
}
|
解法二:迭代
后序遍历真难呀!
代码为:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
|
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> list = new LinkedList<>();
Stack<TreeNode> stack = new Stack<>();
TreeNode pre = new TreeNode();
while (root!=null || !stack.isEmpty()){
while (root!=null){
stack.push(root);
root = root.left;
}
root = stack.pop();
if (root.right==null || root.right==pre){
list.add(root.val);
pre = root;
root = null;
}else {
stack.push(root);
root = root.right;
}
}
return list;
}
}
|
解法三:Morris
不会!不会!不会! 要了命了
但是可以把前序遍历的left变为right right变为left 最后输出的list进行逆转,Collections.recerse(list);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
|
class Solution {
public List<Integer> postorderTraversal(TreeNode root){
List<Integer> list = new LinkedList<>();
TreeNode pre = new TreeNode();
while (root!=null){
list.add(root.val);
if (root.right!=null){
pre = root.right;
while (pre.left!=null && pre.left!=root.left){
pre = pre.left;
}
if (pre.left==null) {
pre.left = root.left;
}else {
pre = pre.left;
list.add(pre.val);
}
root = root.right;
}else {
root = root.left;
}
}
Collections.reverse(list);
return list;
}
}
|










