回文串

最长回文子串(leetCode_5)

给你一个字符串 s，找到 s 中最长的回文子串。

示例 1：

输入：s = "babad"
输出："bab"
解释："aba" 同样是符合题意的答案。

示例 2：

输入：s = "cbbd"
输出："bb"

解法一：暴力解法

通过两个for循环遍历字符串s所有的子字符串。定义一个方法，用来判断是否是回文串，如果是，则记录回文串的长度(len)和开始的位置(begin)。因此 最长的回文子串为：s.substring(begin,begin+len);

• 可以只针对大于「当前得到的最长回文子串长度」的子串进行回文验证；
• 当得到了一个更长的回文时，不需要真的做截取。只需要记录「当前子串的起始位置」和「子串长度」。

代码为：

class Solution {
   //暴力解法
    public String longestPalindrome(String s) {
        int n = s.length();
        if (n<2){
            return s;
        }
        int res = 1;
        int begin = 0;
        char[] ss = s.toCharArray();
        for (int i = 0;i<n-1;i++){
            for (int j = i+1;j<n;j++){
                //如果是回文字符串并且长度比之前的长度大，则改变长度，记录开始位置
                if (j-i+1>res && just(ss,i,j)){
                    res = j-i+1;
                    begin = i;
                }
            }
        }
        //回文字符串就是开始位置-开始位置+长度
        return s.substring(begin,begin+res);
    }
    //判断是不是回文字符串
    public boolean just(char []ss,int i,int j){
        while (i<j) {
            if (ss[i] != ss[j]) {
                return false;
            }
            i++;
            j--;
        }
        return true;
    }
}

解法二：动态规划方法

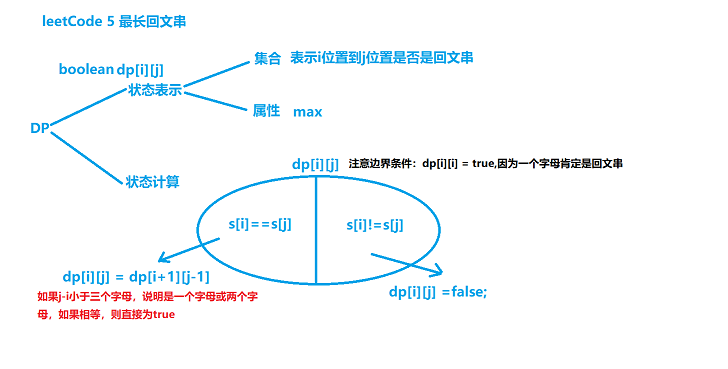
代码为：

class Solution {
   //动态规划 dp[i][j]:表示位置i到位置j是否是回文串
    public static String longestPalindrome(String s) {
        int n = s.length();
        if (n<2){
            return s;
        }
        char[] ss = s.toCharArray();
        boolean dp[][] = new boolean[n][n];
        //处理动态规划的边界条件，本身到本身都是回文串
        for (int i = 0;i<n;i++){
            dp[i][i] = true;
        }
        int res = 1;
        int begin = 0;
        for (int r = 1;r<n;r++){
            for (int l = 0;l<r;l++){
                //如果左端和右端不相等，则直接为false
                if (ss[l]!=ss[r]){
                    dp[l][r] = false;
                }else {
                    //如果是同一个元素或者两个相等的元素，则为true
                    if (r-l<3){
                        dp[l][r] = true;
                    }else {
                        //否则根据dp[l+1][r-1]来判断
                        dp[l][r] = dp[l+1][r-1];
                    }
                }
                //如果是回文串，并且比最大长度大，则更新最大值，记录开始位置
                if (dp[l][r] && r-l+1>res){
                    res = r-l+1;
                    begin = l;
                }
            }
        }
        return s.substring(begin,begin+res);
    }
}

解法三：中心扩散法

「中心扩散法」的基本思想是：遍历每一个下标，以这个下标为中心，利用「回文串」中心对称的特点，往两边扩散，看最多能扩散多远。

注意： 扩散时，回文串长度是奇数或偶数时，中心扩散不一样，所以要分开研究。

奇数时：中心字符串为一个字符，

偶数时：中心字符串为两个字符。

可以设计为：

• 如果传入重合的下标，进行中心扩散，此时得到的回文子串的长度是奇数；
• 如果传入相邻的下标，进行中心扩散，此时得到的回文子串的长度是偶数。

代码为：

class Solution {
    String ans = "";
    public String longestPalindrome(String s) {
        for (int i = 0; i < s.length(); i++) {
            // 回文子串长度是奇数,最中间是同一个数,所以取一个就行
            helper(i, i, s);
            // 回文子串长度是偶数,取两个数字
            helper(i, i + 1, s);
        }
        return ans;
    }
    public void helper(int m, int n, String s) {
        while (m >= 0 && n < s.length() && s.charAt(m) == s.charAt(n)) {
            m--;
            n++;
        }
        // 注意此处m,n的值循环完后  是恰好不满足循环条件的时刻
        // 此时m到n的距离为n-m+1，但是mn两个边界不能取 所以应该取m+1到n-1的区间  长度是n-m-1
        if (n - m - 1 > ans.length()) {
            //substring要取[m+1,n-1]这个区间 
            //end处的值不取,所以下面写的是n不是n-1
            ans = s.substring(m + 1, n);
        }
    }
}